8.Q.1 Quiz 1
When Models Meet Data : Quiz 1
최대가능도
가능성이 가장 높은 모수를 찾는 방법인 최대가능도 추정법 또는 최대우도법(Maximum Likelihood Estimation; MLE)이라고 한다.
정규분포의 모수에 대한 최대가능도추정.
특별히 확률변수 $X$가 연속형 확률변수이고 우리가 잘 알고 있는 정규분포(가우시안 분포)를 따른다면 아래와 같이 평균 $\mu$와 분산 $\sigma^2$, 두 개의 변수로 모수가 구성할 수 있다.
\[\theta = (\mu, \sigma^2)\]평균과 분산을 모르는 정규분포에 최대가능도추정법을 적용하여 모수를 추정하도록 하겠습니다. 정규분포에서 $n$개의 표본 ($x_1, x_2, \cdots, x_n$) 을 독립적으로 추출한다고 했을 때 각 표본의 표본분포는 아래와 같이 표현할 수 있다. ($i=1, \cdots, n$)
\[f_{X_i}(x_i;\theta) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right) , \,\,i=1, \cdots, n\]그러면 독립적으로 추출한 전체 $n$개의 표본에 대한 우도함수(likelihood)는 아래와 같다.
\[P(x|\theta) = \prod_{i=1}^{n}f_{X_i}(x_i;\theta)= \prod_{i=1}^{n}\frac{1}{\sigma\sqrt{2\pi}} \exp \left( -\frac{(x_i-\mu)^2}{2\sigma^2} \right)\]양변에 $log$를 취하여 로그우도함수를 구하면, 아래와 같이 전개된다.
\[L(\theta|x) = \log P(x|\theta) = \sum_{i=1}^{n}\log\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right)\] \[L(\theta|x) = \sum_{i=1}^{n}\left[ \log\left( \exp(-\frac{(x_i-\mu)^2}{2\sigma^2}) \right) - \log\left( \sigma\sqrt{2\pi} \right) \right]\]첫 번째로 $L(\theta | x)$를 모평균 $\mu$에 대해 편미분하면, 아래와 같이 계산되며 미분계수가 0이 되어 최댓값을 갖게 하는 $\mu$를 찾을 수 있다.
\[\frac{\partial L(\theta|x)}{\partial \mu} = -\frac{1}{2\sigma^2}\sum_{i=1}^{n}\frac{\partial}{\partial \mu}\left(x_i^2-2x_i\mu+\mu^2\right)\] \[=-\frac{1}{2\sigma^2}\sum_{i=1}^{n}\left(-2x_i+2\mu\right)\] \[=\frac{1}{\sigma^2}\sum_{i=1}^{n}(x_i-\mu) = \frac{1}{\sigma^2}\left(\sum_{i=1}^{n}x_i-n\mu\right) = 0\]미분계수가 0이 되게 하는 $\mu$ 값은 다음과 같다.
\[\hat{\mu} = \frac{1}{n}\sum_{i=1}^{n}x_i = \bar{x}\]따라서, 최대우도(또는 최대로그우도)를 만들어주는 모평균의 추정량은 바로 표본평균 $\bar{x}$이다.
이번에는 $L(\theta | x)$를 모표준편차 $\sigma$에 대해 편미분하면, 아래와 같다.
로그가능도 함수 $L$을 $\sigma$로 편미분한 후, 편미분계수가 0이 되게 하는 $\sigma$(또는 $\sigma^2$)를 구해보자.
\[\frac{\partial L(\theta|x)}{\partial \sigma} = -\frac{n}{\sigma} - \frac{1}{2}\sum_{i=1}^{n}\left(x_i-\mu\right)^2\frac{\partial}{\partial\sigma}\left(\frac{1}{\sigma^2}\right)\] \[\hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^{n}\left(x_i-\mu\right)^2 =s^2\]따라서, 최대우도(또는 최대로그우도)를 만들어주는 모분산의 추정량은 표본분산 $s^2$이다.
최대가능도 추정법에 의한 정규분포의 기댓값은 표본평균 과 같고 분산은 (자유도가 아닌 데이터의 수로 나눈, 편향) 표본분산과 같다.
최대가능도추정의 실습
연속형 확률변수 $X$가 정규분포를 따른다고 가정하자. 모분산은 1이라는 사실을 알고 있고 모평균을 모르는 상황에서 모평균을 추정해야 한다.
이 때, 우리에게 $x_0 = 1$이라는 샘플을 하나 갖고 있는데
$x_0 =1$일 때, 어떤 평균(모수)에 대해서 가장 큰 가능도(Likelihood)를 갖는지 확인해보자.
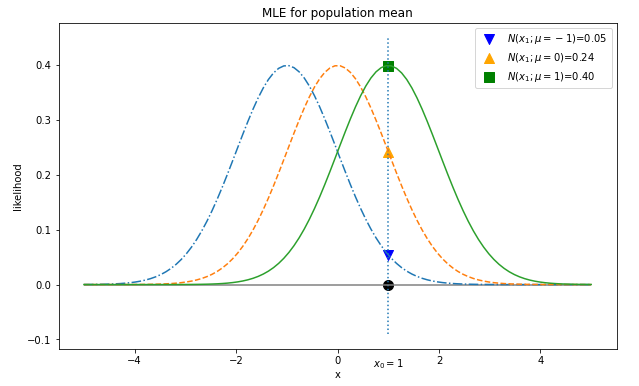
$\mu = -1, 0, 1$ 이렇게 세 가지의 경우의 정규분포를 scipy.stats.norm를 사용해서 그려보자
import numpy as np import scipy as sp import matplotlib.pyplot as plt from scipy.stats import norm plt.figure(figsize=(10,6)) x = np.linspace(-5, 5, 100) p1 = sp.stats.norm(loc=-1).pdf(1) p2 = sp.stats.norm(loc=0).pdf(1) p3 = sp.stats.norm(loc=1).pdf(1) plt.scatter(1, p1, s=100, c='blue', marker='v', label=r"$N(x_1;\mu=-1)$={:.2f}".format(np.round(p1, 2))) plt.scatter(1, p2, s=100, c='orange', marker='^', label=r"$N(x_1;\mu=0)$={:.2f}".format(np.round(p2, 2))) plt.scatter(1, p3, s=100, c='green', marker='s', label=r"$N(x_1;\mu=1)$={:.2f}".format(np.round(p3, 2))) ### START CODE HERE (3 line) ''' plt.plot과 sp.stats.norm를 사용하여, 아래와 같은 그래프를 그려야 한다. ''' ### END CODE HERE plt.scatter(1, 0, s=100, c='k') plt.vlines(1, -0.09, 0.45, linestyle=":") plt.hlines(0, -5, 5, colors='gray', linestyle="-") plt.text(1-0.3, -0.15, "$x_0=1$") plt.xlabel("x") plt.ylabel("likelihood") plt.legend() plt.title("MLE for population mean") plt
정답
아래와 같은 그래프를 그려야 한다.