파라미터 추정
Chapter 3 : Parameter Estimation
-
목차
Maximum Likelihood Estimation(최대 우도 추정법)
Maximum Likelihood Estimation(최대 우도 추정법)의 아이디어는 데이터에 적합한 모델을 찾을 수 있도록 하는 파라미터 함수를 정의하는 것 이다.
확률변수 $x$로 설명할 수 있는 데이터와 $\theta$에 관한 확률 밀도 $p(x|\theta)$일 때, negative log-likelihood function은 다음과 같다.
\[\mathcal{L}_{\boldsymbol{x}}(\boldsymbol{\theta})=-\log p(\boldsymbol{x}|\boldsymbol{\theta})\]$\mathcal{L}_{\boldsymbol{x}}(\boldsymbol{\theta})$는 고정된 $x$에서 파라미터 $\theta$에 대한 함수를 의미한다.
반대로 고정된 $\theta$에 대한 확률 밀도 $p(x|\theta)$는 데이터 $x$를 관측할 확률을 알려준다.
독립된 데이터셋 $(\mathcal{Y}={y_{1}, \ldots, y_{N}})$ 와 $(\mathcal{X}={x_{1}, \ldots, x_{N}})$ 이 있을 때, 이 데이터 셋의 우도는 각 개별 데이터의 우도의 곱으로 표현할 수 있다.
\[p(\mathcal{Y}|\mathcal{X}, \boldsymbol{\theta})=\prod_{n=1}^{N} p\left(y_{n}|\boldsymbol{x}_{n}, \boldsymbol{\theta}\right)\]최적화 관점에서 곱으로 계산할 경우, 많은 계산이 요구되므로 log를 씌워 곱을 합으로 변경하는 것이 더 계산이 빠르고 쉽다. 그래서 머신러닝에서는 아래와 같은 negative log-likelihood를 사용한다.
\[\mathcal{L}(\boldsymbol{\theta})=-\log p(\mathcal{Y}|\mathcal{X}, \boldsymbol{\theta})=-\sum_{n=1}^{N} \log p\left(y_{n}|\boldsymbol{x}_{n}, \boldsymbol{\theta}\right)\]위에서 언급했듯이, $\mathcal{L}(\boldsymbol{\theta})$는 $\theta$에 대한 함수이므로, $\mathcal{L}_{\boldsymbol{x}}(\boldsymbol{\theta})$를 최소화 하기 위한 적합한 파라미터 $\theta$를 찾아야 한다.
아래 그림은 주어진 데이터를 이용하여, 파라미터에 대한 최대 우도 추정법의 결과를 검은 선으로 표현한 것 이다. MLE 같은 경우, 관찰한 값에 따라 값이 잘 변하기 때문에 극단적인 경우를 관찰한다면 문제가 생길 수도 있다. 그렇기 때문에 표본의 크기가 상당히 커야하고 데이터의 양이 적으면 과적합될 수 있다.
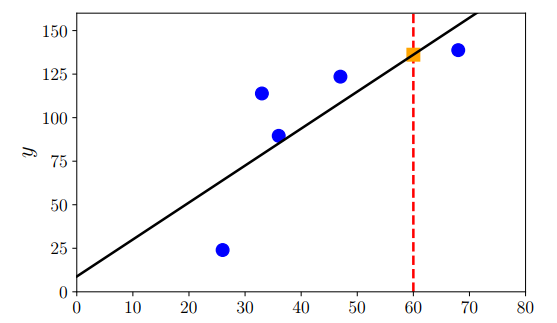
Maximum A Posteriori Estimation(최대 사후 확률 추정법)
MAP는 MLE의 단점을 해결하기 위한 방법이다.
파라미터 $\theta$에 대한 사전 지식이 있을 때, 데이터 $x$를 관측한 후에 이를 토대로, 주어진 x에 대한 파라미터 $\theta$에 대한 분포를 구할 수 있다.
조금 더 자세히 설명을 하면, $x$에 대한 사전 확률 $p(x)$와 파라미터 $\theta$에 대한 사전 확률 $p(\theta)$, 그리고 우도인 $p(x|\theta)$를 이용하여, 파라미터 $\theta$에 대한 사후 확률 $p(\theta|x)$을 구할 수 있다.
\[p(\theta|x) = \frac{p(x|\theta)p(\theta)}{p(x)}\]파라미터 $\theta$를 찾는 것이 목표이기 때문에, $\theta$와 독립적인 $x$의 확률을 무시한다면 아래와 같이 정리할 수 있다.
\[p(\theta|x) \propto p(x|\theta)p(\theta)\]
아래 그림은 주어진 데이터에 대한 MAP와 MLE의 차이를 보여주는 그래프이다. MAP의 경우 정규화 효과처럼 파라미터를 원점에 가깝게 biases를 더해주는 효과가 있다.
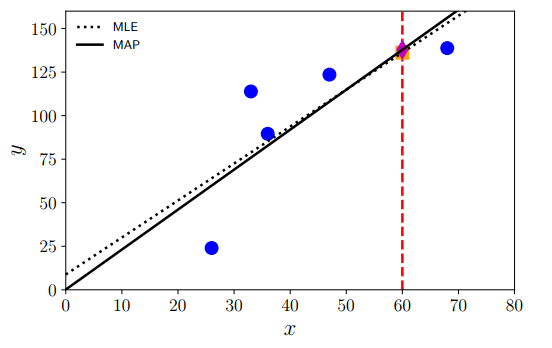
Model Fitting
fitting은 모델 파라미터를 최적화/학습하여 어떤 loss function을 최소화 하는 것을 의미한다.
우리의 목표는 아래의 그림과 같이 트레이닝 데이터셋을 통해서 $M_(\theta)$가 알려지지 않은 모델 $M^{*}$에 최대한 가깝게 최적화 하는 것이다.
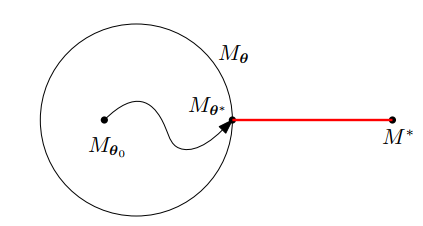
과적합(overfitting)은 파라미터화된 모델 클래스가 너무 많아서 $M^{*}$에서 생성된 데이터셋을 모델링할 수 없고 트레이닝 데이터에만 딱 맞는 경우를 의미한다. 이런 경우 대부분 파라미터의 수가 많다.
과소적합(underfittinf)은 파라미터화되니 모델 클래스가 적어서 생기는 문제이다. 트레이닝 데이터를 충분히 학습하지 못해서 $M^{*}$에 가까운 모델을 생성할 수 없는 경우이다.