확률 분포
Introduction : Probability and Distributions
Edited by / 김주원 (Kim-Ju-won) 
확률의 개념
확률(probability)를 대략적으로 설명하자면 불확실성(uncertainty)에 대한 연구라고 말할 수 있다.
확률은 또한 사건이 발생할 비율 혹은 사건이 발생할 믿음의 정도라고 볼수도 있다. 이렇게 만들어진 확률을 실험상에서 어떤 일이 발생할 정도를 측정하는데 활용된다.
확률 변수와 확률 분포
확률 변수의 개념
Chapter1에서 언급했듯이, 종종 데이터, 기계 학습 모델, 모델의 예측값들의 불확실성(uncertainty) 정량화한다.
이 불확실성을 정량화하는 작업은 확률변수(random variable)를 필요로 한다. 확률변수(Random Variable)란 임의의 실험에 대한 결과와 우리가 관심있는 특성들의 집합을 맵핑(mapping)해주는 일종의 함수이다.
확률 분포
확률 변수를 이용해서 특정한 결과값이 일어날 확률을 측정하는것을 확률 분포(Probability)라고 부른다.
확률 분포는 아래와 같이 다른 개념을 이해하기 위한 하위 개념으로 활용된다.
- 8.4 확률적 모델링(probabilistic modeling)
- 8.5 그래프 모형(graphical models)
- 8.6 모형 선택(model selection)
다음장부터 확률 공간(probabilty space)를 정의하기 위한 표본 공간(the sample space), 사상(event), 사상의 확률(probability of an event)등 세가지 개념을 배우며, 해당 개념과 확률 변수와 어떤 관계가 있는지 살펴볼 것이다.
여기서 타이트하게 개념을 설명하는 것은 개념 넘어에 있는 직관을 방해할 수 있기 때문에 의도적으로 간단하게 개념을 설명하고 있다.
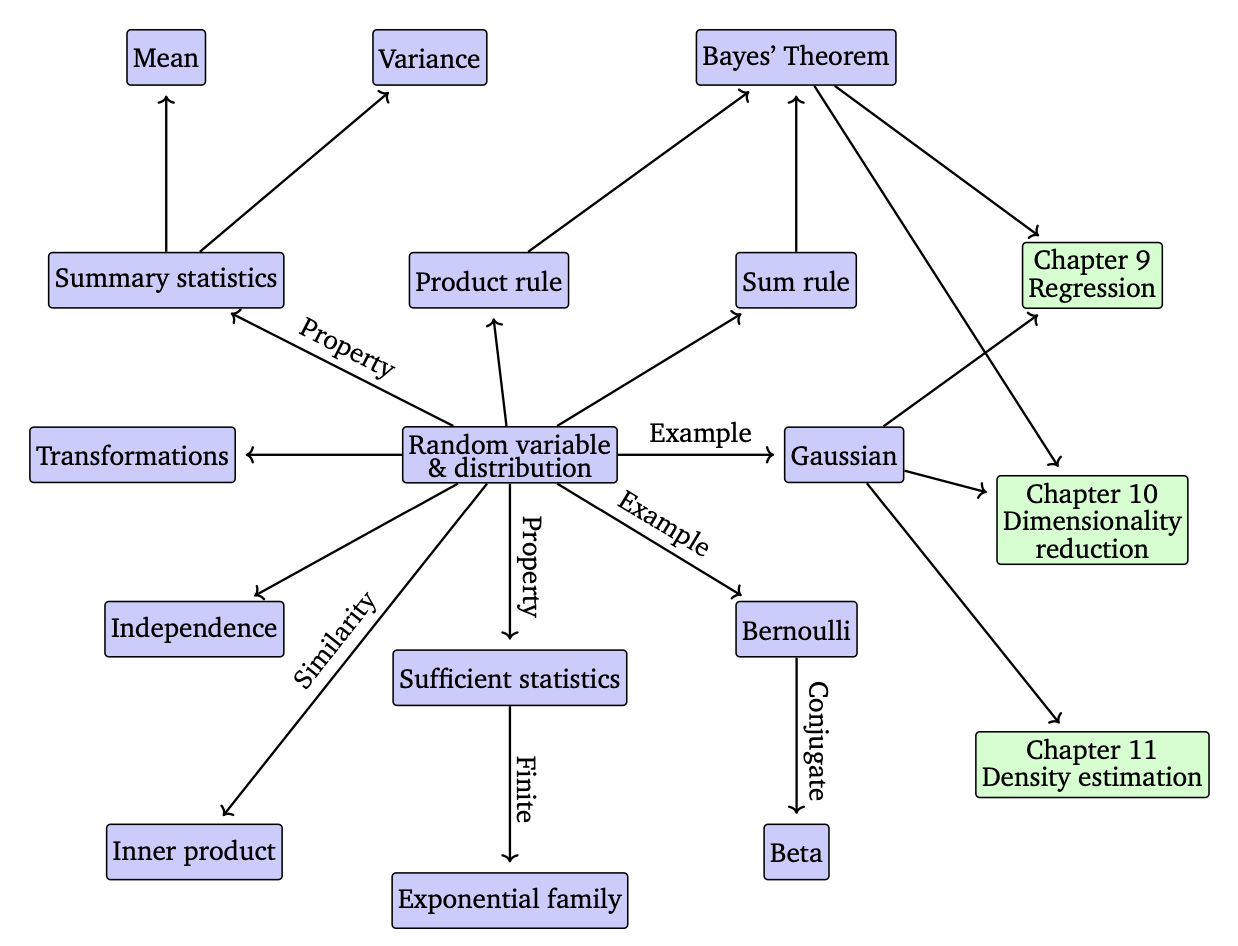
아래 다이어그램은 이 Chapter6 확률분포에서 배우는 개념들의 관계를 도식화한 것이다.
그림1 CHAPTER 6 확률분포 다이어그램
