9. Q.1 Quiz 1
Linear Regression : Quiz 1
-
목차
! 잠깐 !
-
본 페이지의 예제 코드에서는 실행되지 않는 기능이 빠져있을 수 있습니다.
-
아래 링크를 통해 본 페이지보다 원활한 과제 진행 환경을 경험해보세요.
- Week 9 Quiz 보러가기
- Content > Week 9 Directory에 들어가주세요!
Week 9
회귀(Regression)의 정의
-
이번 챕터에서는 이전 Chapter 2, 5, 6, 7 개념을 이용하여 선형회귀(Linear Regression) 또는 곡선 피팅(curve fitting)에 대해서 다룰 것이다.
-
회귀(Regression)는 $x \in \mathbb{R}^d$ 를 만족하는 입력 $x$를 $f(x) \in R$에 맵핑하는 함수 $f$를 찾는 것을 목표로 한다.
- 이 챕터에서는 $x_n$이 훈련 세트(training Set)로 주어지고
-
이에 상응하는 잡음(noise)가 섞인 관측 $y_n = f(x_n)+\epsilon$이 주어졌다고 가정한다.
- 이 챕터 전체에서 평균이 0인 가우시안 노이즈(Gaussian Noise)를 가정한다. 회귀 모델의 목적은 단순히 훈련 데이터에 대해 모델링할 뿐만이 아니라 훈련 데이터에 주어지지 않은 값에 대해서도 잘 예측할 수 있도록 설계 하는 것이다.(Chapter 8 참고)
필요한 library import
import numpy as np import matplotlib.pyplot as plt import scipy.linalg from sklearn.linear_model import LinearRegression import warnings warnings.filterwarnings('ignore')
Exercise 1. 선형 회귀 함수 만들기(Linear Regression)
다음을 만족하는 $x,y$가 있다고 가정하자 \(p(y|x,\theta) = \mathcal{N}(y|f(x), \sigma^2)\)
여기서 입력은 $x \in R_D$ 을 만족하고 $y \in R$ 로 노이즈가 섞인 함수값이며 타겟(target)이다. 우도함수를 이용하여, x와 y의 함수적 관계를 표현한 식은 아래와 같다.
\[y = f (x) + \epsilon\]$\epsilon \sim \mathcal{N}(0,\sigma^2)$는 독립이며, 평균이 0이고 분산이 $\sigma^2$인 가우시안 분포를 따른다. 회귀의 목적은 정확한 데이터를 생산하고 일반화 시키는 $f$와 가장 가까운 혹은 비슷한 함수를 찾는 것이다. 즉, 함수를 통해 주어진 데이터를 생산할 수 있어야하고, 해당 함수는 그러한 데이터를 잘 일반화한 형태여야 된다는 것을 의미한다.
그리고 이러한 형태의 꼴로 나타낼 수 있는 선형회귀 함수를 주어진 데이터를 이용해 만들어보자
1.1 Exercise
선형회귀 식은 다음과 같다.
\[y = \theta X + b\]주어진 데이터를 이용하여 함수를 표현해보자.
# 데이터 x = np.array([3,7,11,15,18,27,29,30,30,31,31,32,33,33,34,36,36, 36,37,38,39,39,39,40,41,42,42,43,44,45,46,47,50]) y = np.array([5,11,21,16,16,28,27,25,35,30,40,32,34,32,34,37,38, 34,36,38,37,36,45,39,41,40,44,37,44,46,46,49,51]) # 식 xbar = np.mean(x) ybar = np.mean(y) ## theta 구하기 ## your code (1 line)## ## ## your code (1 line)## ## # 회귀 직선 그리기 xfit = np.linspace(0,55,100) yfit = theta * xfit + b plt.scatter(x,y) plt.plot(xfit,yfit,'r') plt.show() print('b1=', b1, 'b0=', b0) vectors
1.2 Exercise
- 위 식을 scikit-learn의 Linear regression 함수를 이용하면 손쉽게 그려줄 수 있다.
## 데이터 x = np.array([[3],[7],[11],[15],[18],[27],[29],[30],[30],[31],[31],[32],[33],[33],[34],[36],[36]]) y = np.array([[5],[11],[21],[16],[16],[28],[27],[25],[35],[30],[40],[32],[34],[32],[34],[37],[38]]) ## LinearRegression의 fit함수 활용 ## your code (1 line)## # 회귀 직선 계수 print(reg.intercept_[0]) # b print(reg.coef_[0][0]) # theta(slope) plt.scatter(x,y) plt.plot(x,reg.predict(x),'r') plt.show()
Exercise 2 : MAP 추정 파라미터
2.1 RMSE 구하기
다항식의 평가에 있어서 RMSE(root-mean-squared-error)를 사용하려고 한다. 이를 먼저 정의하자.
\[RMSE = \sqrt{ \frac{1}{N} \sum_{n=1}^N (y_n - y^{pred}_n)^2 }\]def RMSE(y, ypred): ## YOUR CODE (1line) # rmse = # END Code return rmse
2.2 Maximum likelihood estimator 정의
우리는 maximum likelihood estimator를 다음과 같이 얻어 낼 수 있습니다.
\[\theta^{ML} = ( \Phi^T \Phi + \kappa I)^{-1} \Phi^T y\]위의 식을 통해 Maximum Likelihood estimator를 정의하자
def nonlinear_features_maximum_likelihood(Phi, y): kappa = 1e-08 # stability를 위해 추가 D = Phi.shape[1] ### Your Code Pt = None # Phi^T*y PP = None # Phi^T*Phi + kappa*I # maximum likelihood estimate C = scipy.linalg.cho_factor(PP) theta_ml = scipy.linalg.cho_solve(C, Pt) # inv(Phi^T*Phi)*Phi^T*y return theta_ml
다음과 같이 $ \phi (x) $ 를 정의하자
\[\phi (x) = \begin{bmatrix} 1 \\ x \\ x^2 \\ x^3 \\ \vdots \\ x^{K-1} \end{bmatrix} \subseteq \mathbb{R}^K\]def poly_features(X, K): # X: inputs of size N x 1 # K: degree of the polynomial # computes the feature matrix Phi (N x (K+1)) X = X.flatten() N = X.shape[0] #initialize Phi Phi = np.zeros((N, K+1)) # Compute the feature matrix in stages for k in range(K+1): ### Your Code Phi[:,k] = None return Phi
###데이터 생성 def g(x, sigma): p = np.hstack([x**0, x**1, np.sin(x)]) w = np.array([-1.0, 0.1, 1.0]).reshape(-1,1) return p @ w + sigma*np.random.normal(size=x.shape) sigma = 1.0 alpha = 1.0 N = 20 np.random.seed(42) X = (np.random.rand(N)*10.0 - 5.0).reshape(-1,1) y = g(X, sigma) plt.figure() plt.plot(X, y, '+') plt.xlabel("$x$") plt.ylabel("$y$");
2.3 MAP 추정 파라미터 정의하기
MAP 추정 파라미터는 다음과 같이 정의 할 수 있습니다. 남은 코드를 채워주세요
\[\theta^{MAP} = (\Phi^T \Phi + \frac{\sigma^2}{\alpha^2}I)^{-1} \Phi^T y\]Hint)
- $ I $ = np.eye(Phi.shape[1])
def map_estimate_poly(Phi, y, sigma, alpha): # Phi: training inputs, Size of N x D # y: training targets, Size of D x 1 # sigma: standard deviation of the noise # alpha: standard deviation of the prior on the parameters # returns: MAP estimate theta_map, Size of D x 1 D = Phi.shape[1] PP = None #YOUR CODE theta_map = scipy.linalg.solve(PP, Phi.T @ y) return theta_map
# get the MAP estimate K = 8 # polynomial degree # feature matrix Phi = poly_features(X, K) theta_map = map_estimate_poly(Phi, y, sigma, alpha) # maximum likelihood estimate theta_ml = nonlinear_features_maximum_likelihood(Phi, y) Xtest = np.linspace(-5,5,100).reshape(-1,1) ytest = g(Xtest, sigma) Phi_test = poly_features(Xtest, K) y_pred_map = Phi_test @ theta_map y_pred_mle = Phi_test @ theta_ml plt.figure() plt.plot(X, y, '+') plt.plot(Xtest, y_pred_map) plt.plot(Xtest, g(Xtest, 0)) plt.plot(Xtest, y_pred_mle) plt.legend(["data", "map prediction", "ground truth function", "maximum likelihood"])
이제 우리는 앞서 정의한 RMSE를 활용하여 우리는 MAP가 최대 우도법에서 발견된 OVERFITTING을 얼마나 완화시켰는지 알아볼 수 있다.
K_max = 12 # this is the maximum degree of polynomial we will consider assert(K_max < N) # this is the latest point when we'll run into numerical problems rmse_mle = np.zeros((K_max+1,)) rmse_map = np.zeros((K_max+1,)) for k in range(K_max+1): # feature matrix Phi = poly_features(X, k) # maximum likelihood estimate theta_ml = nonlinear_features_maximum_likelihood(Phi, y) # predict the function values at the test input locations (maximum likelihood) y_pred_test = 0*Xtest Phi_test = poly_features(Xtest, k) ypred_test_mle = Phi_test @ theta_ml # RMSE on test set (maximum likelihood) rmse_mle[k] = RMSE(ytest, ypred_test_mle) # MAP estimate theta_map = map_estimate_poly(Phi, y, sigma, alpha) # Feature matrix Phi_test = poly_features(Xtest, k) # predict the function values at the test input locations (MAP) ypred_test_map = Phi_test @ theta_map # RMSE on test set (MAP) rmse_map[k] = RMSE(ytest, ypred_test_map) plt.figure() plt.semilogy(rmse_mle) # this plots the RMSE on a logarithmic scale plt.semilogy(rmse_map) # this plots the RMSE on a logarithmic scale plt.xlabel("degree of polynomial") plt.ylabel("RMSE") plt.legend(["Maximum likelihood", "MAP"])
grading_inverse(inverse)
3. 베이지안 선형회귀(Bayesian linear regression)
3.1 사후 분포(Posterior distribution)
posterior distribution은 다음과 같이 구할 수 있다.
\[\begin{align} p(\theta|\mathcal{X}, \mathcal{Y}) = \mathcal{N}(\theta|m_N, S_N) \\ S_N = (S_0^(-1) + \sigma^(-2)\Phi^T\Phi)^(-1) \\ m_N = S_N(S_0^(-1)m_0 + \sigma^(-2)\Phi^Ty) \\ \end{align}\]
1) 위 식을 사용하여 training set에 대한 $ m_N, s_N $ 을 구하는 posterior distribution 함수를 정의한다.
2) 정의한 함수를 사용하여 test set에 대한 posterior prediction을 진행하고자 한다.
3) 최종적으로 test set에 대한 Bayes linear regression 의 결과를 관찰한다.
Posterior distribution을 구하기 위해 필요한 Training dataset과 prior vairiance 및 noise variance는 다음과 같다.
prior_var = 2.0 # variance of the parameter prior (alpha^2). We assume this is known. noise_var = 1.0 # noise varianc`e (sigma^2). We assume this is known. pol_deg = 3 # degree of the polynomial we consider at the moment Ntrain = 10 Xtrain = np.random.uniform(high=5, low=-5, size=(Ntrain,1)) # training inputs, size Nx1 y = g(X, np.sqrt(noise_var)) # training targets, size Nx1
위 정보들을 활용하여 posterior distribution의 mean와 variance를 구하는 함수는 다음과 같다.
def post_dist(Xtrain, y, K, prior_var, noise_var): # Xtrain: training inputs, size N x D # y: training targets, size N x 1 # K: degree of polynomial we consider # prior_var: prior variance of the parameter distribution # sigma: noise variance jitter = 1e-08 # increases numerical stability Phi = poly_features(Xtrain, K) # N x (K+1) feature matrix Pt = Phi.T @ y # Phi*y, size (K+1,1) PP = Phi.T @ Phi + jitter*np.eye(K+1) # size (K+1, K+1) # parameter posterior iSN = (np.eye(K+1)/prior_var + PP/noise_var) # posterior precision SN = scipy.linalg.pinv(noise_var*np.eye(K+1)/prior_var + PP)*noise_var # posterior covariance mN = scipy.linalg.solve(iSN, Pt/noise_var) # posterior mean return (mN, SN)
위 함수를 활용하여 posterior distribution의 파라미터 mean와 파라미터 variance 를 구한다.
### START CODE HERE (1 line) theta_mean, theta_var = ### END CODE HERE
3.2 사후 예측(Posterior Prediction)
posterior predictive distribution은 다음과 같이 구할 수 있다.
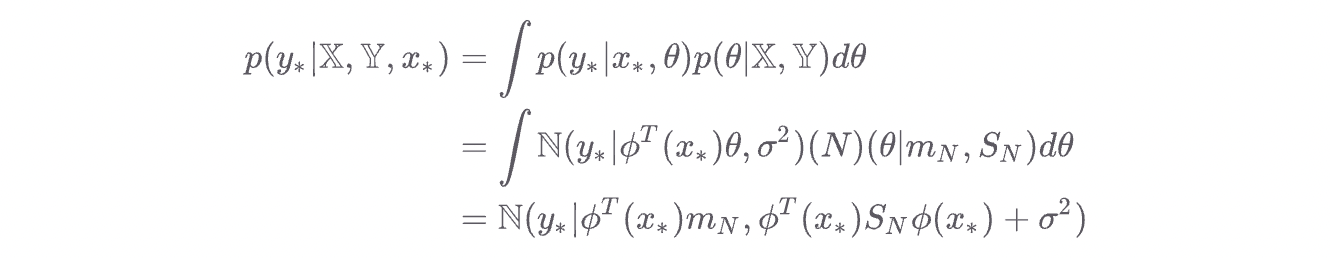
앞서 구한 posterior distribution의 mean과 variance를 사용하여 test set에 대한 posterior prediction을 진행하도록 한다.
# Test inputs Ntest = 200 Xtest = np.linspace(-5, 5, Ntest).reshape(-1,1) # test inputs
# predictive distribution (Bayesian linear regression) Phi_test = poly_features(Xtest, pol_deg) # N x (K+1) # mean prediction ### START CODE HERE (1 line) mean_blr = Phi_test @ theta_mean ### END CODE HERE # variance prediction ### START CODE HERE (1 line) ### END CODE HERE
앞서 testset에 대한 Posterior prediction의 결과는 다음과 같이 확인할 수 있다.
# plot the posterior plt.figure() plt.plot(X, y, "+") var_blr = np.diag(cov_blr) conf_bound1 = np.sqrt(var_blr).flatten() conf_bound2 = 2.0*np.sqrt(var_blr).flatten() conf_bound3 = 2.0*np.sqrt(var_blr + sigma).flatten() plt.fill_between(Xtest.flatten(), mean_blr.flatten() + conf_bound1, mean_blr.flatten() - conf_bound1, alpha = 0.1, color="k") plt.fill_between(Xtest.flatten(), mean_blr.flatten() + conf_bound2, mean_blr.flatten() - conf_bound2, alpha = 0.1, color="k") plt.fill_between(Xtest.flatten(), mean_blr.flatten() + conf_bound3, mean_blr.flatten() - conf_bound3, alpha = 0.1, color="k") plt.legend(["Training data","BLR"]) plt.xlabel('$x$'); plt.ylabel('$y$');