벡터 공간
Chapter 4 : Vector Spaces
지금까지 연립 방정식들을 살펴보고, 어떻게 풀 수 있는지에 대한 방법들을 알아보았다.
앞에서 알아본 내용을 바탕으로 연립 방정식은 행렬로 간단하게 표현할 수 있다는 것을 확인했다.
이번 챕터에서는 벡터로 이루어지는 벡터 공간에 대해 자세히 살펴보도록 하겠다.
벡터 공간(Vector Spaces)은 두 벡터의 연산을 통해 만들 수 있는 공간의 집합을 의미한다.
자세히 알아보자면, 두 벡터의 덧셈과 스칼라 곱을 성립하는 벡터들의 집합을 벡터 공간 또는 선형 공간이라고 한다.
이 때 벡터 공간의 요소들은 모두 벡터이며, 벡터 공간은 다음과 같은 8가지 조건을 만족한다.
-
벡터의 합에 대해
-
$a + b = b + a$ : 교환(commutative)법칙
-
$(a + b) + c = a + (b + c)$ : 결합(associative) 법칙
-
$a + 0 = a$ : 항등원
-
$a + (-a) = 0$ : 역원
-
-
스칼라 곱에 대해
-
$c(a + b) = ca + cb$ : 분배법칙
-
$(c + k)a = ca + ka$ : 분배법칙
-
$c(ka) = (ck)a$
-
$1a = a$
-
그룹(Group)
이 책에서는 벡터공간에 대해 자세히 설명하기에 앞서, 먼저 그룹의 개념을 설명하며 내용을 전개해 나간다.
그룹(Group) 이라는 개념은 컴퓨터 사이언스 영역에서 중요한 역할을 한다.
집합(Sets) 연산에 기반이 되는 프레임워크를 제공한다던지, 암호학, 코딩 이론, 그래픽 등의 분야에서 사용된다.
그룹이란 집합에 포함된 원소간의 연산(Operation)이 해당 집합에 속하는 것을 의미한다.
이를 연산에 대해 닫혀있다(Closure)라고 표현하며 연산자(Operator)는 한개 존재한다.
그룹은 결합 법칙(Associativity) 이 성립하고, 항등원(Neutral element) 가 존재하며, 역원(inverse element) 가 존재한다.

다음 예제를 보며 같이 살펴보자.
$(\mathbb{Z}, +) \rightarrow g $ : 정수는 덧셈에 관하여 닫혀있다.
$(\mathbb{N}_0, +)$ : 0을 포함한 자연수는 역원이 존재하지 않기에 그룹(group)이 아니다.
벡터 공간(Vector Spaces)
벡터 공간은 $V = (V,+,\cdot )$ 로 표현할 수 있다.
위의 수식에서의 $V$ 는 집합을 의미하며, 이 집합의 원소는 벡터이다.
$+$ 는 $V \times V (inner \; operation) \rightarrow V$ 을 의미하고 벡터 덧셈이라고 하며,
$\cdot$ 은 $\mathbb{R} \times V (outer \; operation)\rightarrow V$ 을 의미하며 스칼라 곱셈이라고 한다.
즉, $V$ 는 집합 $V$ 내의 연산 뿐만 아니라 $R$ 영역에 있는 스칼라와의 외부 연산에도 닫혀있다는 것이다.
여기에서 그룹과 다른 부분이 명료하게 드러다는데,
그룹은 집합에 포함된 내부 연산에서만 작용하지만, 벡터 공간은 그렇지 않는다는 점이다.
이렇게 맞닿는 부분이 존재하기에 벡터공간을 설명하기 전에 그룹을 먼저 설명한 이유가 아닐까 싶다.
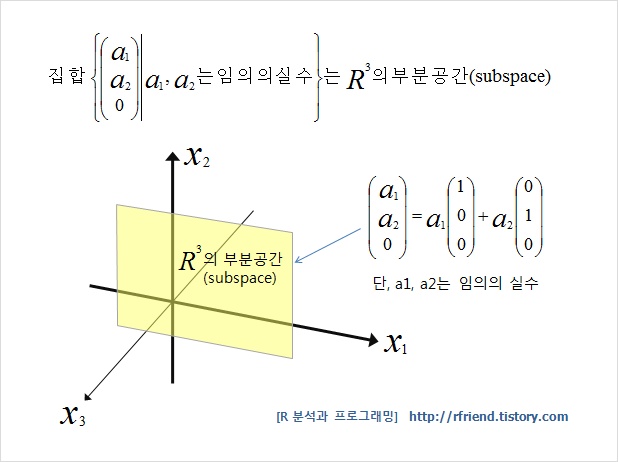
부분공간(subspace)
벡터 공간 $V$ 의 부분집합인 $H$ 가 다음을 만족할 때 부분공간(subspace)이라고 한다.
$u, v$ 는 $V$ 에 속하는 임의의 벡터이다.
-
$V$ 에 속하는 영벡터(zero vector)가 $H$ 의 원소이다.
-
$u, v \in H,\; u + v \in H,\; v + u \in H$
-
$u \in H$ 이고 임의의 스칼라 $c$ 에 대해서 $cu \in H$.
그림5 벡터의 부분 공간