함수에서의 내적 곱
Chapter 7 : Inner Product of Function
Edited by / 박은비 (bluvory) 
Inner Product of Functions
지금까지는 finite-dimensional vector에 대한 inner product만 해왔는데. 이번 장에서는 function에 대한 inner product에 대해 다룬다. 기존의 finite-dimensional vector에 대한 inner product는 다음과 같다
그림1 벡터의 inner product
\[\color{red}{a} \cdot \color{blue}{b} = \sum_{i=1}^{n} \color{red}{a}_{i} \color{blue}{b}_{i} = \color{red}{a}_{1} \color{blue}{b}_{1} + \color{red}{a}_{2} \color{blue}{b}_{2} + \cdots + \color{red}{a}_{n} \color{blue}{b}_{n}\]여기서 계산한 값이 0이 된다면 두 벡터는 orthogonal, 즉 직교한다고 한다.
비슷하게 두 함수의 inner product 식은 다음과 같이 정적분으로 정의 된다.
그림2 함수의 inner product
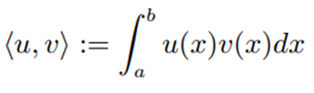
기존에 다뤘던 벡터의 inner product와 마찬가지로 정적분한 값이 0이 된다면 두 함수는 orthogonal하다
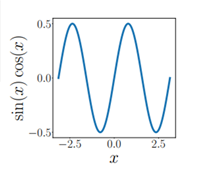
다음은 함수의 inner product에 대한 예제이다. 다음 그래프는 $sin(x)cos(x)$이다. $u=sin(x), v=cos(x), f(x)=u(x)v(x)$라 할 때 가 되므로 $sinx, cosx$가 orthogonal한 것을 알 수 있다
그림3 $sin(x)cos(x)$
