투영 관점에서의 PCA
Chapter 3 : Projection Perspective
-
목차
Projection Perspective
지금까지는 데이터를 투영했을 때 더 많은 정보가 보존되도록 maximum variance를 갖는 basis vector를 찾는 과정을 통해 PCA 알고리즘을 설명하였다.
이 장에서는 앞선 방법과 다르게 투영했을 때 생기는 error(=information loss)가 최소가 되는 투영을 찾는 과정을 통해 $B$를 구하고자 한다.
Setting and objective
투영을 통해 $B$를 찾는 과정은 다음과 같이 세부 목표로 나뉠 수 있다.
- 어떤 투영을 했을 때 loss가 최소가 되는가?
- 어떤 principal subspace 위로 투영해야 최소가 되는가?
- 투영했을 때의 정보 손실은 얼마나 되는가?
이러한 논의를 위해, 데이터 $x$가 놓여있는 차원 $\mathbb{R}^D$에 대해 orthonormal basis (ONB) $B = (b_1, b_2, \cdots, b_D )$가 있다고 가정하면 $x$ 를 다음과 같이 표현할 수 있다.
\[x = \sum_{d=1}^{D} \zeta_d b_d = \sum_{m=1}^{M} \zeta_m b_m + \sum_{j=M+1}^D \zeta_j b_j, \tag{10.26}\]또한 $x$를 $U = span \left[ b_1, b_2, \cdots, b_M \right]$인 $U \subseteq \mathbb{R}^D ,~~dim(U)=M$ 위로 투영되었다고 했을 때, 투영된 (차원 축소된) 데이터 $\tilde{x}$ 는 수식(10. )과 같이 표현할 수 있으며, 이때 우리가 앞서 논의했던 코드 $z_m$ 는 $\tilde{x}$가 $x$와 가장 가까워질 때의 $\zeta_m$ 이다.
즉,
\[\tilde{x} = \sum_{m=1}^{M} z_m\boldsymbol{b}_m \in U \subseteq \mathbb{R}^D, \tag{10.27}\]라고 표현할 수 있으며, $x_n$ 에 대한 $\tilde{x}_n$ 은
\[\tilde{x}_n := \sum_{m=1}^{M} z_{mn}\boldsymbol{b}_m = \boldsymbol{B} z_n \in \mathbb{R}^D, \tag{10.28}\]으로 표현할 수 있다. 이때 $z_n := [z_{1n}, z_{2n}, \cdots, z_{Mn} ] ^\textsf{T} \in \mathbb{R}^M$ 이고, $(b_1, b_2, \cdots, b_M )$은 각각 $\tilde{x}_n$ 을 표현하기 위한 coordinates vectors라고 할 수 있다.
이때 손실(error)이 최소가 되는 $z_n$ 과 $B$를 찾기 위한 objective function은 다음과 같이 정의할 수 있다.
\[J_M := {1\over N} \sum_{n=1}^N \lVert{x_n - \tilde{x}_n}\rVert^2, \tag{10.29}\]Finding Optimal Coordinates ($z_n$)
[그림 5] Optimal projection to minimize information loss
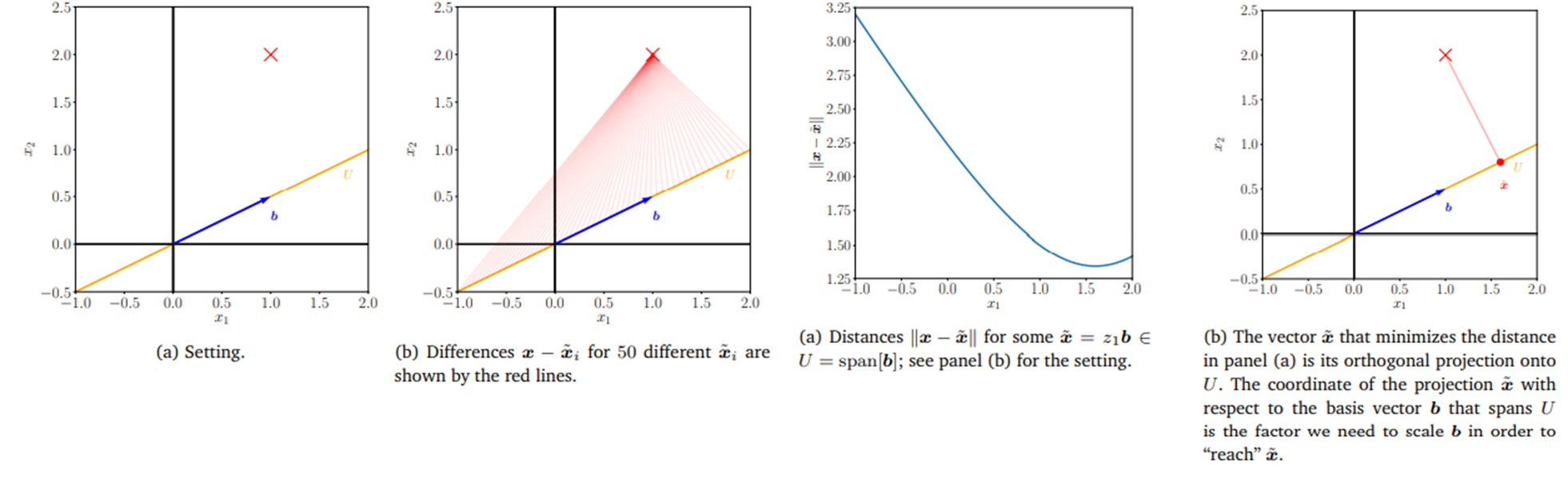
[그림 5]에서 볼 수 있듯이, 주어진 데이터를 $b$ 위에 어떤 식으로 투영하느냐에 따라 데이터가 유지되는 정도가 달라진다.
따라서 “어떤 투영이 가장 손실이 적은가” 에 대해서 알아보려면 coordinates vectors $(b_1, \cdots, b_M)$가 정해졌을 때 손실이 최소가 되는 $z_n$을 구해야 한다. 즉, objective function을 $z_n$에 대해 미분하여 최소가 되는 점을 찾아볼 수 있다. 즉,
\[{\partial J_M\over\partial z_{in}} = {\partial J_M\over\partial \tilde{x}_n}{\partial \tilde{x}_n \over\partial z_{in}} , \tag{10.30a}\] \[{\partial J_M\over\partial \tilde{x}_n} = - {2 \over N}(x_n - \tilde{x}_n)^\textsf{T}\in\mathbb{R}^{1\times D} , \tag{10.30b}\] \[{\partial \tilde{x}_n \over\partial z_{in}} \overset{(10.28)}= {\partial \over \partial z_{in}}(\sum_{m=1}^M z_{mn}\boldsymbol{b}_m) = \boldsymbol{b}_i \tag{10.30c}\]이므로
\[{\partial J_M \over\partial z_{in}} \overset{\substack{\textsf{(10.30b}) \\ \textsf{(10.30c)}}}{=} - {2\over N} (x_n - \tilde{x}_n)^\textsf{T} \boldsymbol{b}_i \overset{\textsf{(10.28)}}{=} - {2 \over N} ( x_n - \sum_{m=1}^M z_{mn} \boldsymbol{b}_m)^\textsf{T} \boldsymbol{b}_i \tag{10.31a}\] \[\overset{\textsf{ONB}}{=} - {2\over N} (x_n^\textsf{T} \boldsymbol{b}_i - z_{in}\boldsymbol{b}_i^\textsf{T}\boldsymbol{b}_i) = - {2 \over N} ( x_n^\textsf{T}\boldsymbol{b}_i - z_{in}). \tag{10.31b}\]따라서 최적의 $z_{in}$은 미분 값이 0이 되는 지점이므로
\[z_{in} = x_n^\textsf{T}\boldsymbol{b}_i = \boldsymbol{b}_i^\textsf{T}x_n \tag{10.32}\]즉, 최적의 투영은 orthogonal projection이다. 그러므로 $\tilde{x}n$ 은 $x_n$을 ($b_1, \cdots, b_M$)이 span하는 subspace $U$에 orthogonal projection을 한 것과 같으며, ($b{M+1}, \cdots, b_D$)가 span하는 공간과 $U$는 orthogonal ($B$가 ONB라고 가정했으므로)이므로 $z_{in}$은 유일하게 결정된다.
따라서 아래의 수식이 성립한다.
\[\tilde{x} = \boldsymbol{b}_i (\boldsymbol{b}_i^\textsf{T} \boldsymbol{b}_i)^{-1} \boldsymbol{b}_j^\textsf{T}x = \boldsymbol{b}_j \boldsymbol{b}_j^\textsf{T}x \in \mathbb{R}^D \tag{10.33}\] \[\tilde{x} = \boldsymbol{B} ( \underbrace{ \boldsymbol{B}^\textsf{T} \boldsymbol{B}}_{=\boldsymbol{I}})^{-1} \boldsymbol{B}^\textsf{T}x = \boldsymbol{B} \boldsymbol{B}^\textsf{T}x , \tag{10.34}\]Finding basis of the Principal subspace($B$)
그렇다면 어떤 principal subspace 위로 orthogonal projection 해야 최소가 되는가?
이에 대해 답하기 위해 수식을 전개해보면 결과적으로 다음과 같다.
\[J_M = \sum_{j=M+1}^D \boldsymbol{b}_j^\textsf{T} \underbrace{({1 \over N} \sum_{n=1}^N x_n x_n^\textsf{T})}_{=: \boldsymbol{S}} \boldsymbol{b}_j = \sum_{j=M+1}^D \boldsymbol{b}_j^{\textsf{T}}S \boldsymbol{b}_j \tag{10.32}\]이는 즉 평균 제곱 오차가 orthogonal complement of the principal subspace $U^{\bot}$ 에 투영되었을 때의 분산과 같다는 뜻이며, 따라서 아래의 식이 성립한다.
\[J_M = \sum_{j=M+1}^D \lambda_j , \tag{10.32}\]즉, 앞에서 논의했던 바와 같이 orthogonal projection을 했을 때 최소가 되는 $b_1, \cdots, b_M$ 은 공분산행렬 $S$에 대해 가장 큰 $M$개의 eigenvalue에 대응하는 eigenvector이다.
10.2와 10.3에 걸쳐 PCA의 작동 원리에 대해서 이야기하였으며, $X$에 대한 공분산 행렬의 eigendecomposition을 통해 수행할 수 있다는 결론을 얻었다. 이제 10.4장과 10.5장, 10.6장에 걸쳐 실제로 PCA를 어떻게 적용할 것인가에 대해서 논의를 해보도록 하자.