볼록 최적화

Chapter 3 : Convex Optimization

Edited by / 임수형 (sulogc)

볼록 최적화

전역 최적해를 보장하는 최적화 문제에 집중해보자. $ f(\cdot) $ 가 convex이고, $ g(\cdot) $ 과 $ h(\cdot) $ 를 포함하는 제약조건이 볼록 집합(convex set)일 때 이는 볼록 최적화 문제(convex optimization problem)라고 부른다. 이러한 조건 하에서 우리는 강 쌍대성을 갖는다. 강 쌍대성은 쌍대 문제의 최적해와 원시문제의 최적해가 같음을 의미한다.

정의 7.2 $x, y \in \mathcal C $ 와 $ 0 \leq \theta \leq 1 $ 인 $ \theta $ 에 대해 다음을 만족하면 집합 $ \mathcal C $는 볼록 집합 이 된다.

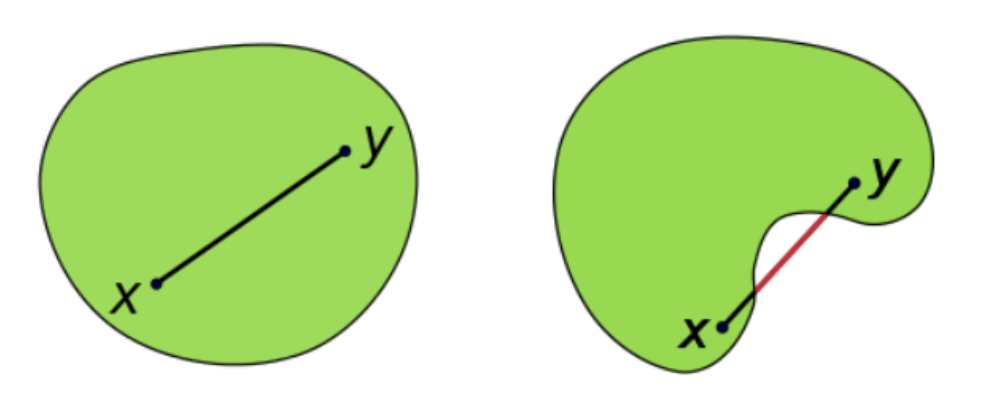
\[\begin{align} \theta x + (1 - \theta) y \in \mathcal C \end{align}\]

볼록 집합은 집합 내에서, 어느 두 점을 연결한 모든 점이 집합에 속하는 것을 의미한다. 다음 그림1 을 통해 볼록 집합과 볼록 집합이 아닌 집합(nonconvex set)의 차이를 알 수 있다.

그림1 convex vs nonconvex set

정의7.3 함수 $ f : \mathbb R^D \mapsto \mathbb R $의 정의역이 볼록 집합이라 하자. 정의역 내 어떤 $ x, y $ 와 $ 0 \leq \theta \leq 1 $ 인 $ \theta $ 에 대해 다음을 만족하면 함수 $ f $ 는 볼록 함수(convex function)라고 한다.

\[\begin{align} f(\theta x + (1 - \theta) y) \leq \theta f(x) + (1 - \theta)f(y) \end{align}\]

다음 식에서 $ g(\cdot) $ 과 $ h(\cdot) $ 은 함수를 잘라 집합을 만든다.

\[\begin{align} \min \limits _{x} \quad & f(x) \\ \text{subject to} \quad & g _i(x) \leq 0 ~ \text{for all} ~ i=1, \dotsc, m \\ \quad & h _j(x) = 0 ~ \text{for all}~ j=1, \dotsc, n && {(7.4)} \end{align}\]

볼록 함수와 볼록 집합의 또 다른 관계로는 볼록 함수를 “채워서” 얻는 집합을 생각해보는 것이다. 볼록 함수는 그릇같은 모양이고 물을 채워넣는 것을 상상해보자. 이후, 채워진 집합이 나올것이며, 이는 볼록 함수의 epigraph 라고 하며, 볼록 집합이 된다.

만약 함수가 미분가능하다면, 이의 그레디언트 $ \nabla _{x}f(x) $에 대한 convexity를 특정화할 수 있다. 함수 $ f(x) $가 convex이기 위한 필요충분조건은 어떠한 두 점 $ x, y $ 에 대해 다음을 만족하는 것이다.

\[\begin{align} f(y) \geq f(x) + \nabla _{x}f(x)^\intercal (y - x) \end{align}\]

함수가 두번 미분 가능하다면(Hessian 존재) 함수가 convex이기 위한 필요충분조건은 $ \nabla^2 _{x}f(x) $ 가 양 정의인 것이다.

요약해서, 제약 최적화 문제인 위 식 7.4 에서 모든 함수 $ f(x) $ 와 $ g _i(x) $ 는 볼록 함수이고, 모든 $h _j (x)=0 $ 은 볼록 집합 인 경우. 위 문제를 볼록 최적화 문제로 볼 수 있다.

선형 계획법

여태까지 보았던 함수가 모두 선형이라고 해보자. 즉,

\[\begin{align} \min \limits _{x \in \mathbb R^d} \quad & c^\intercal x \\ \text{subject to} \quad & A x \leq b \end{align}\]

여기서 $ A \in \mathbb R^{m \times d} $ 이며, $ b \in \mathbb R^m $ 이다. 이는 선형 계획법(linear program)이라 한다. 이는 $ d $ 개의 변수를 갖고 있고 $ m $ 개의 선형 제약조건을 갖고 있다. Lagrangian은 다음과 같이 주어진다.

\[\begin{align} \mathfrak L (x, \lambda) = c^\intercal x + \lambda^\intercal (Ax - b) \end{align}\]

여기서 $ \lambda \in \mathbb R^m $ 은 non-negative 라그랑주 승수로 이루어진 벡터이다. 이를 $ x $ 에 관하여 다시 써보면,

\[\begin{align} \mathfrak L (x, \lambda) = (c + A^\intercal + \lambda)^\intercal x - \lambda b \end{align}\]

$ \mathfrak L (x, \lambda) $ 를 $ x $ 에 대해 미분하고 0으로 두면,

\[\begin{align} c + A^\intercal + \lambda = 0 \end{align}\]

그러므로 라그랑주 쌍대는 $\mathfrak D(\lambda) = - \lambda^\intercal b$가 된다. 우리가 원하는 것은 $ \mathfrak D(\lambda) $ 를 최대화 하는 것이다. 미분하여 0이 되게끔 하는 제약에다가 $ \lambda \geq 0 $ 인 제약을 추가하여 다음과 같은 쌍대 문제를 얻게된다. (원시 문제는 최소화, 쌍대 문제는 최대화)

$ \mathfrak L (x, \lambda) $ 를 $ x $ 에 대해 미분하고 0으로 두면,

\[\begin{align} \max _{\lambda \in \mathbb R^m} \quad & - b^\intercal \lambda \\ \text{subject to} \quad & c + A^\intercal \lambda = 0 \\ & \lambda \geq 0 \end{align}\]

쌍대 문제도 선형 계획법이고, 이번엔 $ m $ 개의 변수를 갖는다. 우리는 $ m $ 이나 $ d $ 중 작은 것을 택해 원시 문제를 풀어도 되고 쌍대 문제를 풀어도 된다.

2차 계획법

제약조건이 아파인 함수(affine function)인 볼록 2차 목적 함수에 대해 고려해보자.

\[\begin{align} \min \limits _{x \in \mathbb R^d} \quad & \frac{1}{2} x^\intercal Q x + c^\intercal x \\ \text{subject to} \quad & A x \leq b \end{align}\]

여기서 $ A \in \mathbb R^{m \times d} $ 이며, $ b \in \mathbb R^m, c \in \mathbb R^d $ 이다. Square symmetric matrix $ Q \in \mathbb R^{d \times d}$ 는 양정의 이므로 목적함수는 convex이다. 이는 2차 계획법(Quadratic program)으로 알려져있다. 이는 $ d $ 개의 변수와 $ m $ 개의 선형제약조건이 있다.

이의 Lagrangian은 다음과 같이 주어진다.

\[\begin{align} \mathfrak L (x, \lambda) & = \frac{1}{2} x^\intercal Q x + c^\intercal x + \lambda^\intercal (A x - b) \\ & = \frac{1}{2} x^\intercal Q x + (c + A^\intercal \lambda)^\intercal x - \lambda^\intercal b \end{align}\]

항을 정리해보자. 미분하고 0으로 놓으면,

\[\begin{align} Q x + (c A^\intercal \lambda) = 0 \end{align}\]

$ Q $ 가 역행렬이 존재한다고 하자.

\[\begin{align} x = Q^\intercal (c + A^\intercal \lambda) \end{align}\]

위 식을 원시 라그랑지안 $\mathfrak L (x, \lambda)$ 로 치환하면, 라그랑지안 쌍대를 얻는다.

\[\begin{align} \mathfrak D (\lambda) = - \frac{1}{2} (c + A^\intercal \lambda)^\intercal Q^{-1} (c + A^\intercal \lambda) - \lambda^\intercal b \end{align}\]

따라서 쌍대 최적화문제가 다음과 같이 주어진다.

\[\begin{align} \max \limits _{x \in \mathbb R^m} \quad & - \frac{1}{2} (c + A^\intercal \lambda)^\intercal Q^{-1} (c + A^\intercal \lambda) - \lambda^\intercal b \\ \text{subject to} \quad & \lambda \geq 0 \end{align}\]

머신러닝에서 quadratic programming을 응용한 사례는 Chapter 12에서 보게 될 것이다.

르장드르-펜첼 변환과 볼록 켤레

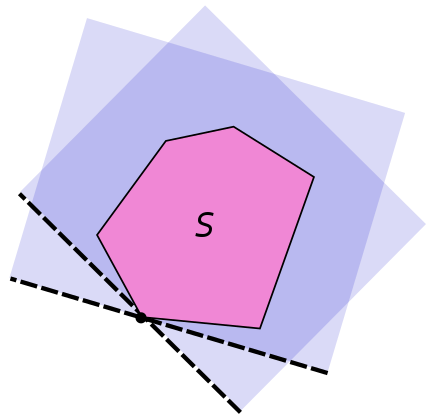
제약 최적화와 라그랑주 승수법 에서 살펴보았던 쌍대에 대해 제약 없이 살펴보도록 하자. 볼록 집합에 대해 유용한 사실 중 하나는 볼록 집합이 볼록 집합의 받침 초평면(supporting hyperplane) 과 동일하게 표현될 수 있다는 것이다. 초평면이 볼록 집합을 가로지르고 한 면을 포함하면 이를 볼록 집합의 초평면 이라고 부른다. 앞서 epigraph를 얻기 위해 볼록 함수에 물을 넣었고, 그 결과가 볼록집합이라 하였다. 그러므로 볼록 함수 또한 이의 초평면을 통해 기술할 수 있다. 이에더해 받침 초평면이 볼록 함수를 단순하게 접하기만 한다면, 이는 그 점에서의 함수의 접선이 된다. 함수에서 $ x _0 $ 에서의 접선은 그레디언트 $\left. \frac{\mathrm{d} f(x)}{\mathrm{d} x} \right \rvert _{x = x _0}$가 된다.

다음은 받침 초평면의 그림이다.

그림2 Supporting Hyperplane

르장드르 변환(Legendre transform)의 개념은 볼록 집합이 이의 받침 초평면을 통해 동일하게 표현할 수 있으므로 볼록 함수 또한 받침 초평면의 그레디언트를 통해 표현할 수 있다는 것이다.

먼저 일반적인 정의를 소개하고, 직관적인 특수한 경우를 소개하겠다. 르장드르 변환은 미분가능한 볼록 함수 $f(x)$ 를 $f(x)$ 의 접선 $s(x) = \nabla _{x} f(x)$와 연관된 함수로 변환한다.(변수에 관한 변환이 아닌 함수에 대한 변환). 르장드르 변환은 볼록 켤레(Convex conjugate)로도 알려져 있으며, 쌍대와 깊게 연관되어 있다.

정의 7.4 함수 $f: \mathbb R^D \mapsto \mathbb R$ 의 볼록 켤레는 다음과 같이 정의된다.

\[\begin{align} f^{*} (s) = \text{sup} _{x \in \mathbb R^D} (\langle s , x \rangle - f(x)) \end{align}\]

여기서 $\text{sup}$는 상한을 의미한다.

여기서 정의한 볼록 켤레는 $f$가 convex하거나 미분가능할 필요가 없다. 정의에선 일반적인 내적을 사용하지만 복잡한 계산을 피하기 위해 스칼라 곱(dot product)을 사용하겠다.

정의 7.4를 기하학적인 관점에서 이해하려면 간단한 1차원의 미분가능한 볼록 함수를 생각하면 된다. 예를 들어 $ f(x) = x^2$ 라 해보자. 이의 초평면은 선이다. 어떤 선 $ y = sx + c $ 를 생각해보자. 우리는 지금 볼록 함수를 이의 초평면을 통해 표현할 것이므로, $ f $ 의 그래프 상의 각 점 $(x _0, f(x _0)) $ 와 gradient를 고정하고, 이를 지나는 $ c $ 의 최솟값을 찾는다. 위 점을 지나는 $ c $ 의 최솟값은 기울기 $ s $ 를 갖는 선이 함수 $f(x) = x^2 $ 을 스쳐 지나가게 된다. 이를 수식으로 표현하면,

\[\begin{align} y - f(x _0) = s(x - x _0) \end{align}\]

$ y $ 절편은 $ -sx _0 +f(x _0) $ 가 된다. $ f $ 의 교차하는 $ y=sx +c $ 에서 $ c $ 의 최솟값은

\[\begin{align} \text{inf} _{x _0} - sx _0 +f(x _0) \end{align}\]

앞서 다룬 볼록 켤레는 이의 negative로 정의된다. 이는 일차원의 convex나 미분가능한 함수가 아닌 어떠한 nonconvex, 미분 불가능한 $ f: \mathbb R^D \mapsto \mathbb R $ 에도 적용 가능하다.

앞서 라그랑주 승수를 이용하여 쌍대 최적화 문제를 유도하였다. 또한 볼록 최적화 문제에 대해 강 쌍대성이 존재하였고, 이를 통해 원시와 쌍대의 해가 일치함을 보였다. 르장드르-펜첼 변환역시 쌍대 최적화 문제로 변환하는데 이용할 수 있다. 또한 함수가 볼록하고 미분가능하면, 이의 상한은 유일하다.

르장드르 변환은 볼록 최적화 문제로 표현할 수 있는 머신러닝 문제에 이용될 수 있다. 특히 각 데이터에 독립적으로 적용되는 볼록 손실 함수의 경우 켤레 손실(conjugate loss)은 켤레 문제로 유도하는데 편리함을 제공한다.

'연속 최적화' 카테고리의 다른 글