실제 PCA의 주요 과정

Chapter 6 : Key steps for PCA in Practice

Edited by / 박상은 (CheezEun)

장성준 (junnei)

목차
1. Key steps for PCA in Practice

Key steps for PCA in Practice

10.4와 10.5에 걸쳐 PCA를 적용하기 위해 고려해야 할 사항들을 살펴보았다. 이번 장에서는 실제로 PCA를 수행할 때 어떤 단계에 걸쳐 수행하는지에 대해 살펴보자.

Mean subtraction

각각의 data 차원에 대해 평균값을 빼준다. 이론상으로는 필요하지 않은 작업이지만, 연산량을 줄이고, 연산 가능 범위를 벗어나는 등 계산하는 데 있어서 발생할 수 있는 문제를 방지해준다
```
 mu = np.mean(x, axis=0)
 x = x - mu
```
Standardization (=scaling)

각각의 data 차원에 대한 standard deviation $\sigma_d$를 나눠준다. 이미지 데이터의 경우엔 각 pixel이 같은 scale을 갖기 때문에 크게 상관없지만, dimension이 각각의 서로 다른 척도 (e.g., 키=m, 체중=kg)로 측정된 경우가 많기 때문에 unit에 대한 편향을 줄이기 위해서 standardization을 수행한다.
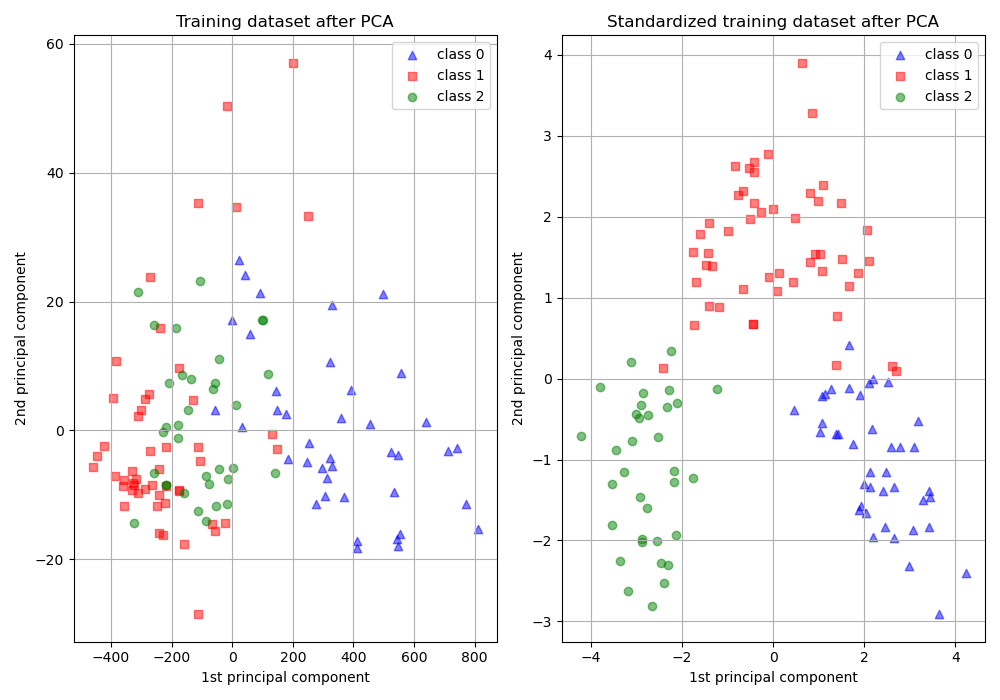
```
 sigma = np.std(x, axis=0)
 x = x / sigma
```
Standardization을 수행하지 않은 데이터는 아래 [그림8]과 같이 전혀 다른 결과를 나타낼 수 있다.

### [그림 8] Example of unstardardization(left) vs. standardization(right)

Eigendecomposition of the covariance matrix

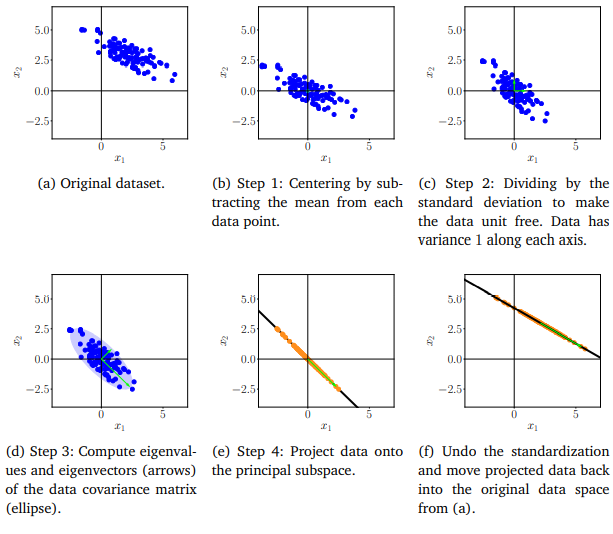
공분산행렬 $S$에 대한 eigenvalues 및 eigenvectors를 구한다. 아래 [그림9] (d)에서는 visualization을 위해 eigenvector에 eigenvalue를 곱한 값을 plot하였으며, $S$를 파란색 타원으로 표현하였다.

 # Eigendecomposition
 S = np.dot(x.T, x)/x.shape[0]
 eigenvalues, eigenvectors = np.linalg.eig(S) # D개의 eigenvalue가 나옴
    
 # SVD
 U, D, eigenvectors = np.linalg.svd(x) 
 eigenvalues = np.square(D)/x.shape[0] # N개의 eigenvalue가 나옴

Variance Ratio 분석

Eigenvalue를 정렬하고, $\sum_{i=1}^M \lambda_i > T$ ($T$는 임계값)을 만족하는 $M$을 찾는다. (np.linalg.eig 및 np.linalg.svd는 이미 정렬되어서 출력된다.)
```
 eigenvalues_ratio = eigenvalues / np.sum(eigenvalues)
 cumulative = np.cumsum(eigenvalues_ratio)
 M = np.argmax(cumulative > T)
```
Projection

Standardized data $x_{*}$를 eigenvector위로 투영한다.
```
 B_trunc = eigenvectors[:,:M]
 x_proj = np.dot(x, B_trunc)
```
Decode

Step 1과 2에서 standardization하면서 변형되었던 부분을 다시 원래 상태로 되돌려 놓는다.
```
 x_tilde = x_proj * sigma + mu
```
### [그림 9] Key Steps of PCA in practice

'차원축소-PCA' 카테고리의 다른 글