요약 통계와 독립

Chapter 4 : Summary Statistics and Independence

Edited by / 유민정 (Minjeong-Yoo)

챕터 소개(Introduction)

종종 확률변수(Random variable)의 set을 요약하거나 확률변수의 쌍을 비교해야 하는 일이 생긴다.

분포(distribution)의 요약통계(summary statistics)을 통해 수치적으로 수행할 수 있으며, 이를 통해 확률변수가 어떻게 행동하는지에 대한 유용한 관점 및 분포의 특징, 요약을 제공한다.

해당 챕터에선 Summary statistics으로 잘 알려진 평균(mean)과 분산(covariance)에 대해 알아본 뒤, 두 확률변수를 비교하는 두 가지 방법에 대해 알아본다.

요약 통계(Summary statistics)

데이터의 속성을 나타내는 숫자값(평균, 표준편차, 분산 등)을 의미한다.
최대한의 정보를 최대한 간단하게 전달하기 위해 관측치의 집합을 요약하는데 사용한다.

평균과 분산(Means and Covariance)

평균과 분산은 확률분포의 특징(기댓값과 퍼짐의 정도)을 나타내는데 유용하게 사용된다.

기댓값(Expected value)

Univariate continuous random variable $X\sim p(x)$의 함수 $g: mathbb{R} \to mathbb{R}$의 기댓값은 다음과 같다. $\begin{align} \mathbb{E}_X[g(x)] = \int_\mathcal{X}g(x)p(x)dx \end{align}$

마찬가지로, discrete random variable $X\sim p(x)$의 함수 $g: mathbb{R}\to mathbb{R}$의 기댓값은 다음과 같다. $\begin{align} \mathbb{E}_X[g(x)] = \sum_{x\in\mathcal{X}}g(x)p(x) \end{align}$

Mean의 정의는 기댓값의 특수한 경우로, $g$가 identity function인 경우에 해당하며 아래와 같다.

평균(Mean)

State $\mathbb{x} \in \mathbb{R}^D$에 대한 확률변수 $X$의 평균은 다음과 같이 정의한다. $\begin{align} \mathbb{E}_X[x] = \begin{bmatrix} \mathbb{E}_{X1}[x_1]\\\vdots\\ \mathbb{E}_{X_D}[x_D] \end{bmatrix} \in \mathbb{R}^D \end{align}$ 여기서 $\mathbb{E}_{X_d}[x_d]$는 $d = 1, \cdots, D$에 대해 다음과 같이 정의된다.

\[\mathbb{E}_{Xd}[x_d] := \left\{ \begin{aligned}\int_\mathcal{X}x_dp(x_d)dx_d \qquad if \ X \ is \ a \ continuous \ random \ variable \\ \sum_{x\in\mathcal{X}}^\mathcal{X}x_ip(x_d = x_i) \qquad if \ X \ is \ a \ discrete \ random \ variable \ \ \end{aligned}\right\} \\\]

아랫첨자 $d$는 $x$의 차원을 의미한다. 적분과 합은 확률변수 $X$의 target space 내의 state $\mathcal{X}$에 대해 시행한다.

Mean, Median, Mode

1차원의 경우, "average"에 대한 직관적인 표현법은 mean 외에 median, mode가 있다.

1. Median
값들을 정렬했을 때, "중앙"에 있는 값을 의미한다. (cdf에선 0.5가 되는 값을 의미)
mean 값보다 사람의 직관에 가까운 값을 제공해준다. (분포가 어느 방향으로 편향되었는지 판단) 편향된 데이터와 이상치 때문에 그릇된 정보를 제공하는 경우를 위해 존재한다. - asymmetric하거나 긴 꼬리가 달린 분포의 경우 사용한다.

2. Mode
가장 빈번하게 등장하는 값을 의미한다. (최빈값) Discrete random variable에서, mode는 발생 빈도가 가장 높은 x의 값으로 정의한다. Continuous random variable에선 density p(x)의 값이 peak일 때의 값으로 정의한다.

공분산(Covariance)

Covariance는 확률변수들이 다른 확률변수와 얼마나 의존되었는지에 대한 직관적인 개념을 제공한다.

단일 변수 공분산 (Univariate Covariance)

Univariate random variables $X, Y \in \mathbb{R}$ 간의 covariance는 $X, Y$ 각각의 평균과 개별 값의 차의 곲의 평균과 같다. $\begin{align} Cov_{X,Y}[x,y] := \mathbb{E}_{X,Y}[(x - \mathbb{E_X}[x])(y - \mathbb{E_Y}[y])] \end{align}$

기댓값의 linearity 성질을 이용해 (4)는 다음과 같이 바꿔쓸 수 있다.

\[\begin{align} Cov[x,y] := \mathbb{E}[xy] - \mathbb{E}[x]\mathbb{E}[y] \end{align}\]

자기자신에 대한 공분산 $Cov[x,x]$는 variance라고 부르며, $\mathbb{V}_X[x]$로 표기한다. Variance의 제곱근은 standard deviation이라고 부르며, $\sigma(x)$로 표기한다.

다변수 공분산(MultiVariate Covariance)

State $x \in \mathbb{R^D}, y \in \mathbb{R^E}$를 갖는 두 Multivariate random variables X, Y에 대한 covariance는 다음과 같이 정의한다.

$Cov[x,y] := \mathbb{E}[xy^T] - \mathbb{E}[x]\mathbb{E}[y]^T = Cov[y,x]^T \in \mathbb{R^{D \times E}}$

분산(Variance)

State $x \in \mathbb{R^D}$와 mean vector $\mu \in \mathbb{R^D}$를 갖는 multivariate random variable $X$에 대한 variance는 다음과 같다.

\[\mathbb{V}_X[x] = Cov_X[x,x] = \mathbb{E}_X[(x-\mu)(x-\mu)^T] = \mathbb{E}_X[x] \mathbb{E}_X[x] \mathbb{E}_X[x]^T\] \[\begin{align} = \begin{bmatrix} Cov[x_1, x_1] && Cov[x_1, x_2] && \cdots && Cov[x_1, x_D] \\ Cov[x_2, x1] && Cov[x_2, x_2] && \cdots && Cov[x_2, x_D] \\ \vdots && \vdots && \ddots && \vdots \\ Cov[x_D, x_1] && \cdots && \cdots && Cov[x_D, x_D] \end{bmatrix} \end{align}\]

$D \times D$ 행렬(6)은 multivariate random variable X의 covariance matrix라고 부른다.
Covariance matrix는 symmetric 하고 positive semidefinite 하며, 데이터의 퍼짐에 대한 정도를 나타낸다.
Covariance matrix의 대각 성분은 marginal에 대한 variance를 포함하고, 대각 성분 이외의 성분은 cross-covariance 성분을 포함하며, $Cov[x_i, x_j]$ for $i,j = 1, …, D, i \ne j$ 로 표현한다.

두 확률 변수 사이의 covariance를 비교하려 하면, 각 확률 변수의 variance의 영향을 받기 때문에 객관적인 비교가 어렵다. 따라서 covariance의 normalized version인 correlation을 사용하여 비교한다.

상관관계(Correlation)

두 확률 변수 X, Y 사이의 correlation 정의는 다음과 같다.

\[corr[x,y] = {Cov[x,y]\over \sqrt{\mathbb{V}[x]\mathbb{V}[y]}} \in [-1, 1]\]

Correlation matrix은 standardized random variable의 covariance matrix, $x\over \sigma(x)$ 와 같다.

그림1 x,y의 평균과 분산 시각화

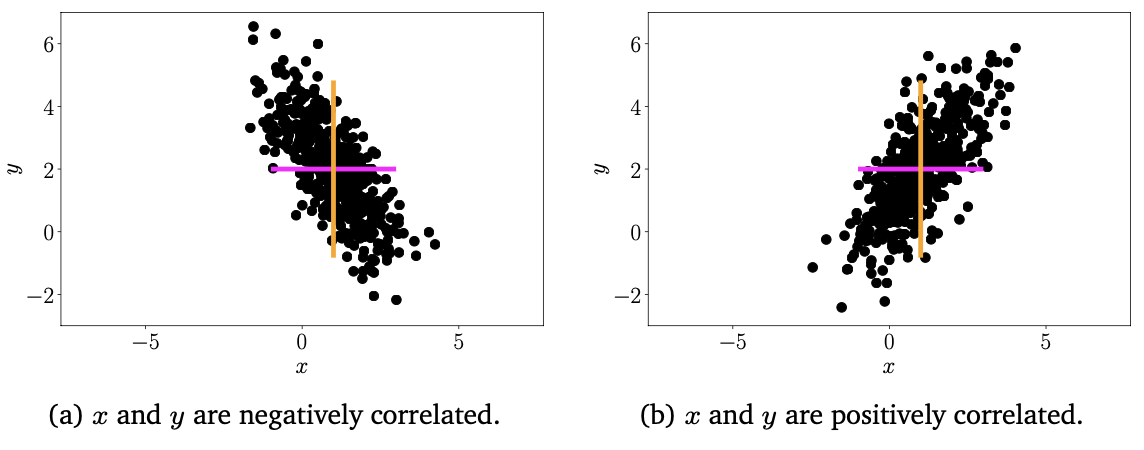
Covariance/Correlation은 두 확률 변수가 어떻게 연관되어 있는지를 나타낸다. 그림 1을 보면 positive correlation $corr[x,y]$은 x값이 커짐에 따라 y 또한 커지는 것을 기대할 수 있다. 반대로, negative correlation은 x값이 증가함에 따라 y값이 감소하는 것을 의미한다.

표본 평균과 분산(Empirical Means and Covariances)

앞에서 다룬 정의들은 엄밀히 말하면 모집단(population) mean과 covariance 이다. 이는 모집단에 대한 실제 통계량을 나타내기 때문이다. 그러나 머신러닝에서는 표본(empirical observation)에 대한 데이터를 다룰 필요가 있다.
특정한 데이터셋이 주어졌을 때 mean에 대한 추정치를 얻을 수 있으며, 이를 empirical mean 혹은 sample mean이라 부른다. 이는 empirical covariance에 대해서도 동일하게 적용된다.

표본평균(Empirical mean)

empirical mean vector는 각 확률 변수에 대한 관측치의 산술평균으로 이루어지며, 다음과 같이 정의한다.

\[\begin{align} \overline{x} := {1 \over N} \sum_{n=1}^Nx_n, \quad x_n \in \mathbb{R}^D \end{align}\]

표본 분산(Empirical covariance)

empirical covariance matrix는 $D \times D$ matrix이며, 다음과 같이 정의된다.

\[\begin{align} \overline{x} := {1 \over N} \sum_{n=1}^N(x_n-\overline{x})(x_n-\overline{x})^T \end{align}\]

특정 데이터셋에 대한 statistics를 계산하기 위해, 실현값(관측값) $x1, …, x_N$와 식 (7), (8)을 사용한다.

분산에 대한 세가지 표현(Three Expressions for the Variance)

해당 챕터에선 single random variable X 에 대해, 앞서 본 empirical formula를 사용하여 variance의 세 가지 표현 방법을 유도하고자 한다. 아래 수식은 적분을 관리해야 한다는 점을 제외하곤 population variance와 동일하며, 분산의 일반적 정의인 “확률변수 $X$와 기댓값의 차이의 제곱근”으로 다음과 같이 정의한다.

\[\begin{align} V_X[x] := \mathbb{E}_X[(x-\mu)^2] \end{align}\]

이때, 식에서 표현한 variance는 새로운 확률 변수 $Z := (X - \mu)^2$ 의 평균값이라고 해석할 수 있다. 경험적으로 식의 variance 를 추정할 때, 우리는 다음의 두 알고리즘에 의존해야 합니다. 1) 데이터를 사용하여 식의 empirical mean을 계산하는 알고리즘, 2) 앞서 구한 추정값 $\hat{\mu}$을 사용하여 variance를 계산하는 알고리즘. 그러나 variance를 raw-score formula 라고 불리는 식으로 재정리하면 두 알고리즘을 거치지 않아도 된다.

\[\begin{align} \mathbb{V}_X[x] = \mathbb{E}_X[x^2] - (\mathbb{E}_X[x]^2) \end{align}\]

식은 “제곱의 평균에서 평균의 제곱을 뺀 값”이라고 표현할 수 있다. 이는 곧 $x_i$ 데이터를 쌓음과 동시에 $x_i^2$을 계산할 수 있다는 점에서 하나의 알고리즘에만 의존한다는 것을 의미한다. ($x_i는 i번째 관측값을 말한다) 그러나 variance의 raw-score formula 식은 수적으로 불안정하다는 점이 있다. 이는 머신러닝에서 bias-variance decomposition를 도출할 때 유용하게 사용된다.

variance의 세 번째 표현방법으로는 모든 관측치 쌍 간의 pairwise(모든 관측치 데이터 간의 최소한 한 번씩을 조합하는 방식) 차이의 합이 있다. 확률변수 X의 실현값으로 관측치 $x_1, …, x_n$이 있을 때, $x_i$와 $x_j$ 쌍 간의 제곱 차를 계산한다. 관련 식은 다음과 같다.

\[\begin{align} {1 \over N^2} \sum_{i,j=1}^N(x_i-x_j)^2 = 2\begin{bmatrix}{1 \over N} \sum_{i=1}^N x_i^2 - ({1\over N} \sum_{i=1}^N x_i)^2 \end{bmatrix} \end{align}\]

위 식은 raw-score formula 식의 2배로 구성된 것을 확인할 수 있다. 이는 기하학적으로 보면, pairwise 거리와 점 집합의 중심으로부터의 거리 사이에 동등성이 있다는 것을 의미한다.

확률변수의 합과 변환(Sums and Transformations of Random Variables)

state $x,y \in \mathbb{R}^D$를 갖는 확률변수 X, Y 가 있을 때 다음 연산이 성립한다.

\[\mathbb{E}[x+y] = \mathbb{E}[x] + \mathbb{E}[y] \\ \mathbb{E}[x-y] = \mathbb{E}[x] - \mathbb{E}[y] \\ \mathbb{V}[x+y] = \mathbb{V}[x] + \mathbb{V}[y] + Cov[x,y] + Cov[y,x] \\ \mathbb{V}[x-y] = \mathbb{V}[x] + \mathbb{V}[y] - Cov[x,y] - Cov[y,x]\]

mean과 covariance는 확률변수의 affine transformation을 수행할 때 유용한 성질들을 유지한다. mean $\mu$와 covariance matrix $\sum$, $x$의 (deterministic) affine transformation $y = Ax + b$를 갖는 확률변수 X가 있는 경우, 확률변수 $y$의 mean vector와 covariance matrix는 다음과 같다.

\[\mathbb{E}_Y[y] = \mathbb{E}_X[Ax+b] = A\mathbb{E}_X[x] + b = A\mu + b \\ \mathbb{V}_Y[y] = \mathbb{V}_X[Ax+b] = \mathbb{V}_X[Ax] = A\mathbb{V}_X[x]A^T = A\sum A^T\]

또한,

\[\begin{align} Cov[x,y] &= \mathbb{E}[x(Ax+b)^T] - \mathbb{E}[x]\mathbb{E}[Ax+b]^T \\ &= \mathbb{E}[x]b^T + \mathbb{E}[xx^T]A^T - \mu b^T - \mu \mu^T A^T \\ &= \mu b^T - \mu b^T + (\mathbb{E}[xx^T] - \mu \mu^T)A^T \\ &= \sum A^T \end{align}\]

여기서, $\sum = \mathbb{E}[xx^T] - \mu \mu^T$ 는 $X$의 covariance가 된다.

통계적 독립( Statistical Independence)

독립(Independence)

두 확률변수 X, Y 에 대해 아래의 식을 만족하는 경우 statistical independence 이라고 한다. $p(x,y) = p(x)p(y)$

만약 X, Y 가 statistical independence인 경우 다음이 성립한다.

\[\begin{align} p(y|x) = p(y) \end{align}\] \[\begin{align} p(x|y) = p(x) \end{align}\] \[\begin{align} \mathbb{V}[x+y] = \mathbb{V}_X[x] + \mathbb{V}_Y[y] \end{align}\] \[\begin{align} Cov_{X,Y}[x,y] = 0 \end{align}\]

마지막 항목인 식의 반대는 성립하지 않을 수 있다. 즉, 두 확률변수가 covariance = 0 의 값을 갖더라도 statistical independence 하지 않을 수 있다. 이는 covariance 가 오직 linear dependence 만을 측정한다는 사실을 알면 된다. 그러므로 nonlinearly dependent인 확률변수들의 covariance는 0의 값을 가질 수 있다.

조건부 독립(Conditional Independence)

두 확률변수 X, Y 가 주어진 Z에 대해 conditionally independent하다는 것은 다음과 동치이다.

\[\begin{align} p(x,y|z) = p(x|z)p(y|z) \quad for \ all \ z \in \mathbb{Z} \end{align}\]

여기서 $\mathbb{Z}$는 확률변수 $Z$의 state에 대한 집합이다. 위 식은 $z$의 모든 값에 대해 참이 성립해야 한다.
식은 $z$에 대한 지식이 주어졌을 때, 분포 $x$와 $y$가 분해된다 라고 이해할 수 있다. 이는 확률의 곱셈규칙을 이용하여 다음의 식을 얻을 수 있다.

\[\begin{align} p(x,y|z) = p(x|y,z)p(y|z) \end{align}\]

식와 식의 우변을 비교해보면, 다음의 관계식을 얻을 수 있다.

\[\begin{align} p(x|y,z) = p(x|z)p(y|z) \end{align}\]

식 또한 조건부 독립에 대해 또 다른 표현식을 나타낸다.

확률 변수 내적( Inner Products of Random Variables)

만약 두 확률변수 X, Y가 uncorrelate 하다면 다음의 식이 성립한다.

\[\begin{align} \mathbb{V}[x+y] = \mathbb{V}[x] + \mathbb{V}[y] \end{align}\]

분산은 제곱을 통해 측정되므로, 이는 피타고라스 정리 $c^2 = a^2 + b^2$와 비슷하게 생기게 된다.
확률변수는 벡터공간 내 벡터로 생각할 수 있으며, 기하학적 성질을 얻기 위해 내적을 정의할 수 있다. zero mean을 갖는 두 확률변수 X, Y에 대해, 아래와 같이 정의하면 내적을 얻을 수 있다.

\[\begin{align} <X,Y> := Cov[x,y] \end{align}\]

확률변수의 길이는 다음과 같다.

\[\begin{align} \parallel X\parallel= \sqrt{Cov[x,x]} = \sqrt{V[x]} = \sigma[x] \end{align}\]

두 확률변수 X, Y 사이의 각도 $\theta$에 대해서는 다음의 식을 얻을 수 있다.

\[\begin{align} cos\theta = {<X, Y> \over {\parallel X \parallel \parallel Y \parallel}} = {Cov[x,y] \over \sqrt{\mathbb{V}[x] \mathbb{V}[y]}} \end{align}\]

이는 즉, 상관관계를 기하학적으로 두 확률변수에 대한 각도로 볼 수 있다는 뜻을 지닌다.

### **그림2** x,y 상관관계 기하학 시각화 {: .no_toc .text-delta }

'확률 분포' 카테고리의 다른 글

```