고차원 미분
Chapter 7 : Higher-Order Derivatives
Edited by / 박은비 (bluvory) 
-
목차
고차원 미분
지금까지 gradient를 다루는데 있어서 first order derivative만을 다루었다 이번 section에서는 higher order derivative에 대해 알아본다
section 5.1.1에서 taylor series를 통해 polynomials를 이용하여 함수를 근사하는 것에 대해 다루었는데 multivariate case에서도 같은 방식을 사용하여 적용할 수 있다. 이와 같은 방식으로 접근하여 higher order derivative를 다루고자 한다 그 전에 관련된 notation에 대해 짚고 넘어가도록 하자
그림1 partial derivative of f
- x에 대한 f의 2차 편도함수
- x에 대한 f의 n차 편도함수
- x에 대한 f의 편도함수에서 y에 대한 편도함수를 구한 것
- y에 대한 f의 편도함수에서 x에 대한 편도함수를 구한 것
Hessian은 모든 이차 편도함수의 모음이다 f(x, y)를 두번 연속적으로 미분 가능할 함수일 경우 다음과 같고 symmetric하다
그림2 Hessian
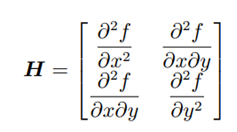
- $▽_{x, y}^2f(x, y)$로 표시
- 일반적으로 $x∈R^n$, $f:R^n→R$, nxn matrix
- f(x, y) 주변의 함수의 곡률(curvature)을 측정