더 읽을거리

Chapter 9 : Further Reading Exercise

Edited by / 박은비 (bluvory)

목차
1. 더 읽을거리
  1. 이 속성은 비선형 동적 시스템(“상태-공간 모형”이라고도 함)에서 온라인 상태 추정을 위해 확장 Kalman 필터(Maybeck, 1979년)에 의해 크게 이용됩니다. (5.181)의 적분을 근사하는 다른 결정론적 방법은 향기가 없는 변환(줄리어 라플라스 및 얼만, 1997) 또는 국소 가우스 근사치에 2차 테일러 시리즈 확장(헤시안 필요)을 사용하는 근사(맥케이, 2003; 비숍, 2006; Murphy, 2012)이다. 모드 주변으로.

더 읽을거리

Magnus and Neudecker (2007) Greiwank and Walther (2003) Griewank and Walther (2008) Elliott (2009)

머신러닝에서 우리는 종종 기댓값을 계산할 필요가 있다, 즉 다음 식을 계산해야 할 필요가 있다

그림1 Calculate Expectation

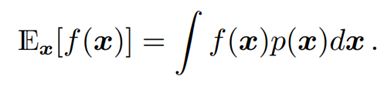
p(x)는 convenient form (Gaussian)이라면 적분은 analytically하게 풀리지 않는다 f의 Taylor series expansion은 가장 근접한 답을 찾을 수 있는 방법이다 p(x)가 Gaussian이라고 가정하고 그다음 first order Taylor series expansion은 nonlinear funciton f를 지역적으로 선형화한다 linear function에서 우리는 p(x)가 가우시안 분포일때의 평균과 표준편차를 계산할 수 있다

이 속성은 비선형 동적 시스템(“상태-공간 모형”이라고도 함)에서 온라인 상태 추정을 위해 확장 Kalman 필터(Maybeck, 1979년)에 의해 크게 이용됩니다. (5.181)의 적분을 근사하는 다른 결정론적 방법은 향기가 없는 변환(줄리어 라플라스 및 얼만, 1997) 또는 국소 가우스 근사치에 2차 테일러 시리즈 확장(헤시안 필요)을 사용하는 근사(맥케이, 2003; 비숍, 2006; Murphy, 2012)이다. 모드 주변으로.

'벡터 미적분학' 카테고리의 다른 글