Sum 법칙, Product 법칙, 베이즈 정리

Chapter 3 : Sum Rule, Product Rule, and Bayes’ Theorem

Edited by / 김주원 (Kim-Ju-won)

배경

확률 이론는 논리적 추론의 확장으로 생각할 수 있다. 이 책의 확률의 규칙은 데이터를 충족함으로써 설계 된다.(Jaynes, 2003, 2장, Section 6.1). 확률론적 모델링(Section 8.4)은 머신러닝의 학습 방법의 원칙 및 기초를 제공한다. 일단 문제 설정 및 데이터의 불확실성에대한 확률 분포(Scection 6.2)를 정의하면, Sum Rule과 Product Rule이라는 두가지 규칙이 있는 것을 확인할 수 있다.

$p(x, y)$는 확률 변수 x, y의 결합분포이다. 확률분포 $p(x)$와 $p(y)$는 대응하는 주변 분포이고, $p(y|x)$는 x가 일어났을 때 y가 일어날 조건부 확률이다. 주변 분포, 조건부 확률, 그리고 확률 분포를 이용하면 Sum Rule과 Product Rule을 도출 할 수 있다.(Section 6.2)

Sum 규칙(Sum Rule)

Sum 규칙(Sum Rule)은 아래와 같이 표현할 수 있다. (확률 변수 $Y$의 Target Space의 원소 $\mathcal{Y}$와 매핑된다.)

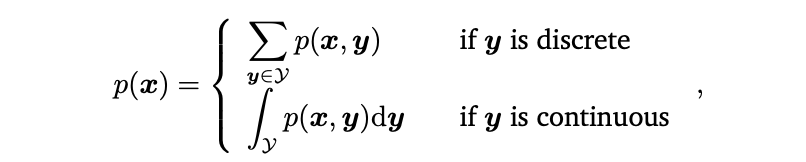
이 식이 의미하는 것은 모든 확률 변수 $Y$의 모든 값 $y$에 대한 합계 혹은 적분 값을 의미한다. 이러한 Sum Rule는 marginalization property 라고 알려져있다. Sum Rule은 또한 주변 확률과 결합 확률을 연관 시킨다. 일반적으로 결합확률은 두 개 이상의 확률 변수를 가지고 있을 때, Sum Rule은 확률 분포의 하위 집합에 적용할 수 있어, 잠재적으로 하나 이상의 확률 변수는 주변 분포를 가지게 된다.

보다 구체적으로, 만약 $x = [x_1 , . . . , x_D ]^T$ 이면 $x_i$를 제외한 모든 확률 변수를 더하거나 적분함으로써 이외의 값은 marginalization property를 갖게된다.

\[p(x_i) =\int_{p(x_1, ..., x_D)}dx_{\i}\]

(\i 는 i만 제외하고 라는 의미로 쓰인다.)

참고1. Sum Rule과 컴퓨터 계산량 문제

확률론적 모델링의 컴퓨터 계산량 문제는 Sum Rule을 적용하면서 발생한다. 많은 양의 이산 확률 변수가 있을 경우, Sum Rule은 고차원의 합 혹은 적분을 하게 된다. 이러한 고차원의 합/적분은 컴퓨터 연산을 어렵게 하며, 얼마나 걸리는지 적당한 시간을 알기 힘들다.

Product 규칙(Product Rule)

두 번째 규칙은 Product Rule으로 다음 식을 이용하여 결합 확률을 조건부 확률과 연관시킨다.

\[p(x, y) = p(y | x)p(x)\]

Product 규칙에서 모든 결합 분포에 있는 두개의 다른 확률 변수는 확률 곱으로 인수분해가 될 수 있음을 알 수 있다. 두 인수는 각각 주변 확률 분포 $p(x)$와 x가 일어날 확률에 대한 y가 일어날 확률인 조건부 확률 $p(y|x)$가 된다. 임의의 $p(x, y)$를 나타내기에 $p(x, y) = p(x|y)p(y)$로도 표현 할 수 있다. 해당 확률은 이산 확률 변수에서는 확률 질량 함수(pmf), 연속 확률 변수에서는 확률 밀도 함수(pdf)로 표현된다.

베이즈 정리(Bayes’ theorem)

그림1 CHAPTER 6 베이즈 정리, 사전확률, 사후 확률, 우도

머신러닝과 베이즈 통계(Bayesian statistics)에서, 우리는 관측되지 않거나 주어지지 않은 확률 변수의 확률 값을 구해야하는 경우가 있다. 관측되지 않은 확률변수 $x$에 대한 사전 지식 사전 지식 $p(x)$와 $x$와 확률 변수 $y$ 의 조건부 확률 $p(y|x)$를 가지고 있다고 가정하자. 만약 y를 관찰수 있으면 우리는 베이즈 정리(Baye’s therorem)을 사용하여 y에 대한 $x$의 어떤 결론(사후 확률, $p(x|y)$)를 구할 수 있다.

베이즈 정리 Bayes’ theorem (Bayes’ rule or Bayes’ law)

\[p(x, y) = p(x | y)p(y)= p(y | x)p(x)\] \[p(x|y)p(y) = p(y|x)p(x)\Leftrightarrow p(x|y) = \frac{p(y | x)p(x)}{p(y)}\]

사전 확률(prior)

$p(x)$는 사전 확률을 의미하며, 어떠한 데이터도 관찰 되지 않은 시점에서 가지고 있는 주관적인 사전 지식이다. 상황에 맞는 사전 확률을 선택해야 하며, 0이 아닌 확률 질량/밀도 함수 값을 가지고 있어야 한다.

우도 (likelyhood)

$p(y|x)$ 는 x,y의 연관성을 나타내고 이산확률분포의 경우 $x$가 주어졌을 때 $y$에 대한 확률이된다. 중요한 것은 $x$의 분포가 아니라 $y$의 확률 분포를 보여준다는 것이다. $y$에대한 x의 우도”, $x$에 대한 y의 확률이라고 한다.

사후 확률(Posterior)

$p(x|y)$은 사후 확률을 의미하며, 베이지안 통계에서 quantity of interest라고 하며, 궁극적으로 구하려는 값이다. $y$가 일어났을 때 $x$의 확률을 의미한다.

marginal likelihood/evidence

\[p(y):= \int p(y|x)p(x) dx \mathbb{E}(X)\]

위 식을 marginal likelihood/evidence라고 부른다. 우변은 평균을 의미한다.(Section 6.4.1)

정의에 의해, marginal likelihood는 (6.23)의 분자를 잠재변수 $x$에 대해 적분한다. 그러므로 marginal likelihood는 $x$에 대해 독립이며, 사후확률 $p(x|y)$가 정규화가된다. 또한, 이는 사전 확률 $p(x)$에 대한 우도 기대값(expected likelihood)로 해석할 수 있다. 사후 확률의 정규화는 Section 8.6에서 배울 베이지안 모델함수에서 중요한 요인이 된다.

참고2. 베이지안(Bayesian Statistics)

베이즈 통계학에서 사후분포는 quantity of interest로, 데이터와 사전확률로부터 가능한 모든 정보를 담고 있다. 사후확률을 따르는 대신, 사후확률의 최대값과 같은 통계량에 관심을 갖는 것도 가능하다. 그러나 이는 정보의 손실을 야기한다. 더 큰 맥락을 생각해보면, 사후확률은 의사결정 시스템에서 사용할 수 있으며, 완전 사후확률을 갖는 것은 매우 유용하며 robust한 결정을 내릴 수 있게된다. 예를 들어 강화학습에서 Deisenroth et al. 2015는 plausible transition functions의 완전 사후확률분포가 매우 빠른 학습(data/sample efficient)을 가능케 했으며, 사후 확률의 최댓값을 이용하는 방법은 일관되게 안 좋은 결론을 도출하였다. 따라서 완전 사후확률분포는 downstream task에서 매우 유용하다고 할 수 있다. 이는 Chapter 9의 선형 회귀의 관점에서 다시 살펴보도록 하겠다.

'확률 분포' 카테고리의 다른 글

```