선형 독립
Chapter 5 : Linear independence
Edited by / 장성준 (junnei) 
-
목차
선형 독립
서로 다른 벡터들의 집합 $S = {v_1, v_2, v_3, … , v_n}$ 에 대해서 $c_1 v_1 + c_2 v_2 + … + c_n v_n = 0$ 을 만족하는 0 이 아닌 $c_1, c_2, … , c_n$ 이 존재하는 경우를 선형종속 이라고 한다.
반대로, $c_k = 0 (k =1,2,…,n) $ 일 때만 위의 조건을 만족하면 선형 독립 이라고 한다.
다음 그림들과 함께 알아보도록 하자.
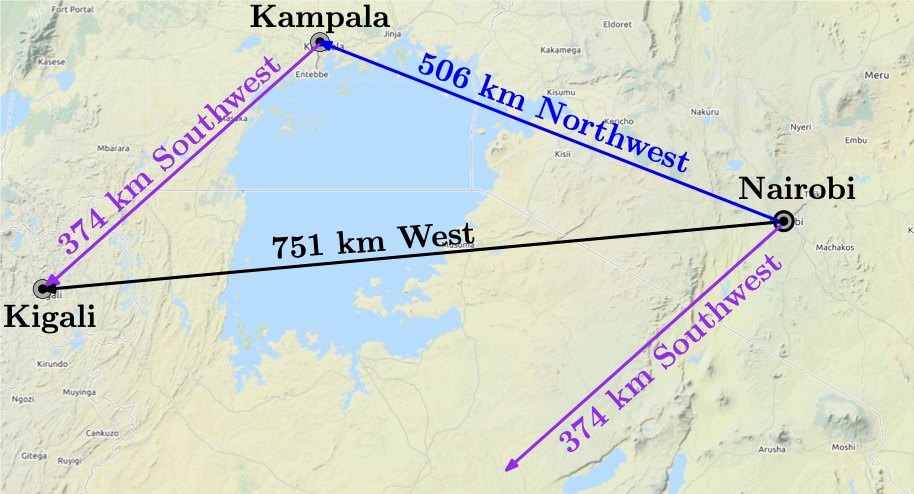
위의 그림에서는 다음과 같은 세가지 벡터를 가지고 있다.
-
$Nairobi \rightarrow Kampala$
-
$Kampala \rightarrow Kigali$
-
$Nairobi \rightarrow Kigali$
여기에서 1) 과 2) 의 벡터는 서로 다른 벡터를 표현할 수 없기 때문에 선형 독립이고, 3)의 벡터는 1) 과 2) 의 선형 결합으로 이루어져 있다.
2차원에서는 벡터가 동일한 직선 위에 존재하면 선형종속이라고 하고, 그렇지 않아야 선형독립이다.
3차원에서는 두 벡터가 이루는 평면 위에 세번째 벡터가 존재하면 선형종속이라고 하고, 그렇지 않아야 선형독립이다.