분산 최대의 관점에서의 PCA
Chapter 2 : Maximum Variance Perspective
-
목차
Maximum Variance Perspective
Why Maximum variance?
이 장에서는 정보의 손실을 최대한 방지하면서 차원을 축소시키는 경우를 다뤄보고자 한다.
이 장에서 가장 핵심적인 개념은,
여러 데이터들에 담긴 정보의 양(information content)은 데이터가 차지하는 공간으로 생각할 수 있다는 점이다.
즉, 데이터를 vector space에 표현했을 때 더 넓은 공간을 점유할수록 데이터가 다양한 정보를 포함하고 있다는 의미이다.
[Chapter 6.4]에서 데이터가 얼마나 흩뿌려져 있는지(how spread of the data)에 대한 지표로서 분산(variance)을 정의하였다.
정보를 최대한 유지하면서 차원을 축소한다는 것은 데이터의 다양성을 보존하면서 데이터의 공통적인 부분을 압축한다는 것이며, 이는 곧 데이터 압축과정에서 분산이 큰 부분은 유지해야 한다는 뜻이다.
[그림 4] Maximum-variance-compressed data is most similar with original data
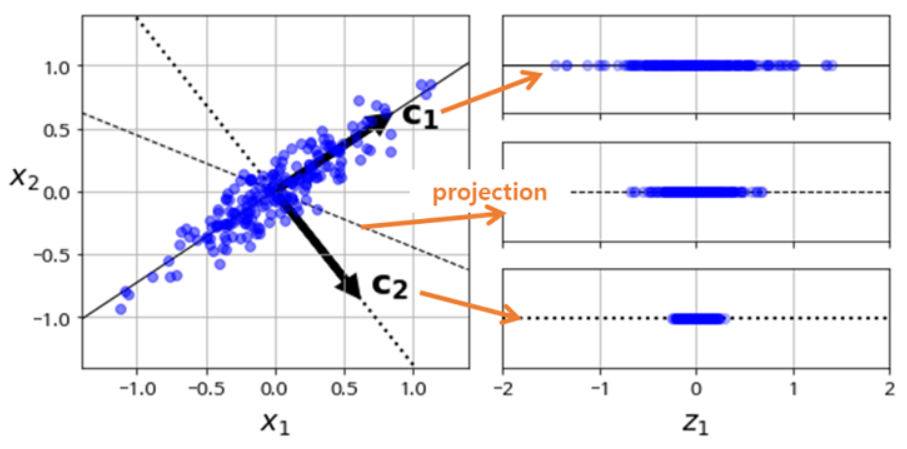
Reference
위 [그림 4]에서 각각의 축 위로 차원 축소를 진행했을 때, 원래 데이터의 정보를 가장 잘 유지시키는 방향은 축소된 데이터의 분산이 가장 크게되는 방향($c_1$)임을 알 수 있다.
이러한 이유로 분산을 크게 유지하는 것이 데이터의 정보를 최대한 유지하는 것이라고 말할 수 있다.
이 후 나올 수식들에서도 분산에 대한 수식 위주로 다룰 것이며,
이 때, 분석하기 쉽도록 분산과 무관한 데이터의 평균($\mu$)은 0이라고 가정하고 진행할 것이다.
Direction with Maximal Variance
우선 가장 간단한 상황을 생각해보자. 데이터를 single vector $b_1 \in \mathbb{R}^D$ 위로 투영(projection)했을 때 분산이 최대가 되도록 하는 $b_1$를 구하기 위해 그때의 분산을 식으로 표현해보면 다음과 같다.
\[V_1 := \mathbb{V}[z_1] = {1\over N} \displaystyle\sum_{n=1}^N z_{1n}^2 \tag{10.9}\]여기서 $z_1$은 모든 데이터 $x$ 를 $b_1$ 위로 투영한 데이터들을 의미하며, 이때 $z_1 \in \mathbb{R}^M$ 이고, $x \in \mathbb{R}^D$, $b_1 \in \mathbb{R}^{D \times M}$이다. 또한,
\[z_{1n} = b_1^\textsf{T}x_n \tag{10.10}\]이고 이는 $x_n$을 $b_1$ 위로 orthogonal projection한 결과가 $z_{1n}$이라는 것을 의미한다.
이제 (10.9)와 (10.10)에 의해
\[V_{1} = {1\over N}\sum_{n=1}^N (b_{1}^\textsf{T} x_n)^2 = {1\over N} \sum_{n=1}^N b_{1}^\textsf{T}x_{n}x_{n}^\textsf{T}b_{1} \tag{10.11}\] \[= b_{1}^\textsf{T}({1\over N} \sum_{n=1}^N x_{n}x_{n}^\textsf{T})b_{1} = b_{1}^\textsf{T}Sb_{1} \tag{10.12}\]으로 표현가능하며, 여기서 $S$는 $X = [x_1, \cdots, x_N]$의 공분산 행렬(covariance matrix)이며 다음과 같다.
\[S = {1 \over N} \displaystyle\sum_{n=1}^N x_n x_n^\textsf{T} \tag{10.13}\]또한, 수식 (10.12)를 통해 알 수 있는 점은, $|b_1 |$에 따라 $V_1$ 도 변화한다는 점이다. 즉, basis vector의 크기를 임의대로 잡으면 정확하게 분산을 비교할 수 없기 때문에 $|b_1|$의 크기를 제한할 필요가 있다. 따라서 우리가 구해야 할 basis vector는 normalized vector이면서, 데이터의 분산($V_1)$을 가장 크게 하는 vector를 찾아야 한다. 이것을 다시 쓰면
\[\begin{align}&\underset{b1}{max}\ b_1^\textsf{T}Sb_1 \\ s&ubject\ to\ \lVert{b_1}\rVert^2 = 1. \end{align}\tag{10.14}\]가 되며, 이에 대한 Lagrangian을 구하면
\[\mathfrak{L}(b_1,\lambda) = b_1^\textsf{T}Sb_1 + \lambda_1 (1-b_1^\textsf{T}b_1) \tag{10.15}\]최대값을 구하는 문제이므로 Lagrangian을 미분해서 0이 되는 지점을 찾으면
\[{\partial\mathfrak{L}\over\partial b_1} = 2b_1^\textsf{T}S - 2\lambda_1 b_1^\textsf{T},\quad {\partial\mathfrak{L}\over\partial \lambda_1} = 1 - b_1^\textsf{T}b_1 , \tag{10.16}\] \[Sb_1 = \lambda_1 b_1, \tag{10.17}\] \[b_1^\textsf{T}b_1 = 1. \tag{10.18}\]따라서 식 (10.14)와 (10.17)에 의해
\[V_1 = b_1^\textsf{T}Sb_1 = \lambda_1b_1^\textsf{T}b_1 = \lambda_1, \tag{10.19}\]다시 말해 분산($V_1$)이 최대가 되도록 하는 basis vector는 $X$의 공분산행렬 $S$의 eigenvector이며, 그때의 분산은 eigenvalue $\lambda_1$이다. 그러므로 분산이 가장 최대가 되도록하는 basis vector를 선정한다는 것은 $S$의 eigenvalue 중에서 가장 큰 eigenvalue와 그에 대한 eigenvector를 구하는 것과 같다.
M-dimensional subspace with Maximal Variance
$m-1$ 차원의 주성분(principal components)를 공분산 행렬 $S$의 가장 큰 $m-1$개의 eigenvalue에 대응하는 eigenvector로서 구했다고 가정해보자. 이제 우리의 목표는 다음 $m$번째 주성분을 찾는 것이며, 이를 위해서는 기존의 데이터 행렬 $X$ 가 아닌 $m-1$ 개의 eigenvector로부터 추출되지 못한 잔여 정보(remaining information)에서 가장 큰 분산을 차지하는 eigenvector를 주성분으로서 선택해야 할 것이다.
( $X = [x_1, x_2, \cdots, x_N] \in \mathbb{R}^{D \times N}$ 이며 각 data가 column으로 표현된다는 것을 명시??)
따라서 잔여 정보 $\hat{X}$를 정의하기 위해 $m-1$ 개의 basis vector로 이루어진 basis $B_{m-1}$와 $\hat{X}$를 다음과 같이 정의하자. 아래 수식(10.23)과 같은 성질을 만족한다.
\[B_{m-1} := \sum_{i=1}^{m-1} b_i b_{i}^\textsf{T} \tag{10.20}\] \[\hat{X} := X - \sum_{i=1}^{m-1} b_i b_{i}^\textsf{T} X = X - B_{m-1} X, \tag{10.21}\]이때 공분산 행렬 $S$는 대칭행렬이기 때문에, $S$의 eigenvector들은 서로 orthonormal basis(ONB)이므로 (10.22), (10.23)와 같은 성질을 만족한다.
\[b_i b_j = \begin{cases} 1 & & (i=j)\\ 0& & (i \neq j)\end{cases} \tag{10.22}\] \[B_{m-1} b_{i} = \begin{cases} b_i && if\quad i<m\\ 0 &&if\quad i \ge m\end{cases} \tag{10.23}\]결론
따라서 $\hat{S} b_m = S b_m = \lambda_m b_m$ 을 만족하며, 이때의 $V_m = \lambda_m$ 이므로 최대 분산을 갖는 데이터를 추출해낸 이후의 잔여 정보 $\hat{X}$ 에서도 eigenvector와 eigenvalue가 유지된다는 뜻이므로, 매번
가장 큰 eigenvalue를 선택하여 압축 → $\hat{X}$ 구함 → 가장 큰 eigenvalue를 선택하여 압축 → $\hat{X}$를 구함 → …
의 과정을 거치지 않아도 된다.
즉,
1) $X$의 공분산 행렬 $S$의 eigenvalue들을 구하고,
2) 그 중 값이 가장 큰 $M$ 개의 egienvalue 및 eigenvector를 선택
의 과정만 거침으로써 PCA를 수행할 수 있다.
또한 PCA 과정에서 얼마나 정보가 보존되는지, 즉 분산이 유지되는지는 다음과 같이 독립된 분산의 합으로 구할 수 있다.
\[V_{M} = \sum_{m=1}^{M} \lambda_m, \tag{10.25}\]이며, 다시 말해 정보 손실율과 정보 보존율은 각각 $1- {V_M \over V_D}$ 와 ${V_M \over V_D}$가 된다.