차원축소 - PCA

Introduction : Dimensionality Reduction with PCA

Edited by / 박상은 (CheezEun)

장성준 (junnei)

차원 축소 - PCA(Dimensionallity Reduction with PCA)

우리가 흔하게 다룰 수 있는 데이터 중에서 이미지, 소리와 같은 데이터들은 대부분 하나의 데이터에 변수가 많은 고차원 데이터(high-dimensional data)이다.

특히나 이미지의 경우 150x150 크기만 되어도 $150^2$, 즉 22,500 개의 변수를 다루어야 하므로 연산량이 많아져 분석을 하는데 어려움이 있고,

데이터를 불러오고 저장하는데에도 많은 메모리를 필요로 한다.

이런 데이터는 심지어 특정한 포맷이 없다면 분석하기 어려울 뿐더러, 데이터의 의미를 파악하기도, 시각화하기도 불가능에 가깝다.

따라서 이러한 고차원 데이터를 최대한 정보 손실 없이 저차원 데이터로 압축하는 방법(차원 축소, dimensionallity reduction)을 이용한다면 데이터의 저장, 연산 과정을 효율적으로 만들 수 있다.

이 챕터에서는 선형 차원 축소를 위한 주성분 분석(PCA)에 대해 이야기하고자 한다.

PCA는 Pearson(1901)과 Hotelling(1933)이 제안했으며 100년이 넘었음에도 여전히 데이터 압축과 데이터 시각화에 유용하게 사용되고 있는 알고리즘이다.

특히 본 사이트의 과제를 통해 PCA가 고차원 데이터에서의 특징을 추출해 패턴을 파악하거나 구조를 식별하는 데도 사용된다는 점에도 집중해서 다루고자 한다.

Independence of dimensions

차원축소의 기본적인 원리는 데이터의 각 차원이 독립적이지 않다는 것에서 기인한다.

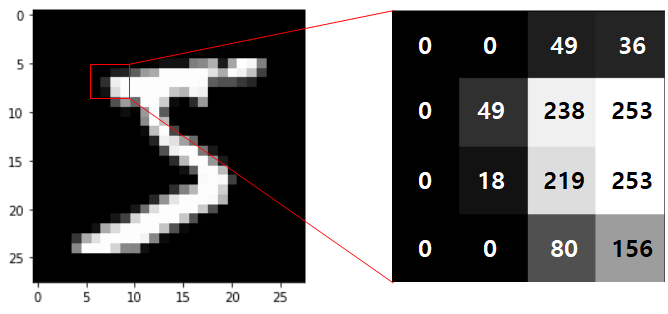
아래 [그림 1]은 MNIST data이며, 오른쪽의 확대된 이미지에서 0 값을 갖는 pixel 주변은 낮은 값을 갖고, 높은 값(253)을 갖는 pixel 주변부는 비슷하게 높은 값을 갖는다는 것을 알 수 있다. 즉, 주변부 차원에 서로 영향을 주고 받는다는 뜻이다.

[그림 1] Example of dependence of dimension with MNIST image

이와 같이 고차원 데이터들은 한 차원이 다른 차원의 조합으로 설명될 수 있거나 서로 상관관계가 존재하는 등,

다른 차원간에 의미가 중복되는 경우가 종종 존재하기에 차원을 축소할 여지가 분명 존재한다.

Example of dimensionallity reduction

그렇다면 독립적이지 않은 차원들을 어떻게 축소시킬 것인가?

예를 들어서 4개의 $\mathbb{R}^2$ 차원의 데이터(즉, basis vector = $\begin{bmatrix} 1 \\ 0 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \end{bmatrix}$)가 다음과 같다고 생각해보자.

\[\begin{bmatrix} 4\\2 \end{bmatrix}, \begin{bmatrix} 8\\4 \end{bmatrix}, \begin{bmatrix} -2\\-1 \end{bmatrix}, \begin{bmatrix} -6\\-3 \end{bmatrix} \tag{10.1}\]

이 데이터들은 각각 2차원 정보를 가지고 있지만 각 차원이 독립적이지 않다. ($x_1 = 2 x_2$ 가 항상 성립)

다시 말해, 모든 데이터가 $\begin{bmatrix} 2\\1 \end{bmatrix}$ 벡터의 실수배로 표현할 수 있으므로

basis vector를 $\begin{bmatrix} 2\\1 \end{bmatrix}$ 로 생각한다면 아래와 같이 1차원 정보로 표현할 수 있다.

\[2,~ 1,~ -1,~ -3 \tag{10.2}\]

이렇듯 2개의 차원이 서로 독립적이지 않다면 이를 이용하여 데이터를 표현하는 차원의 수를 줄일 수 있다.

Example of dimensionallity reduction with noise

그러나 실제로는 대부분의 경우 위의 예시처럼 모든 데이터를 완전히 손실없이 축소하기 어렵다.

그렇다면 이 경우에는 어떻게 축소할 것인가? 아래 예시를 통해 살펴보자.

위의 예시 데이터에서 약간의 노이즈가 추가된 형태이다.

\[\begin{bmatrix} 4.1\\2 \end{bmatrix}, \begin{bmatrix} 8\\3.8 \end{bmatrix}, \begin{bmatrix} -2.01\\-1 \end{bmatrix}, \begin{bmatrix} -6\\-3 \end{bmatrix} \tag{10.3}\]

이 경우에는 위 (10.1)의 예시와는 달리 basis vector를 $\begin{bmatrix} 2\\1 \end{bmatrix}$만을 두고 계산할 수 없다.

따라서 이번 챕터에서 다뤄질 PCA를 이용하면 (10.3)의 데이터를 (10.4)와 같이 표현할 수 있다.

\[\begin{bmatrix} 2.04\\-0.02 \end{bmatrix}, \begin{bmatrix} 3.96\\-0.08 \end{bmatrix}, \begin{bmatrix} -1.004\\0.002 \end{bmatrix}, \begin{bmatrix} -3\\0 \end{bmatrix} \tag{10.4}\]

변환된 데이터를 살펴보면, 두번째 차원에 대한 정보가 매우 작은 값을 가지므로 다음과 같이 근사하면 정보 손실을 최소화하면서 차원을 축소할 수 있다.

\[2.04 ,~ 3.96,~ -1.004,~ -3 \tag{10.5}\]

즉, 데이터를 온전히 보존하면서 축소하지는 못해도 손실을 최소화하면서 줄이는 것은 가능하며, 축소된 데이터는 다음과 같이 basis vector ($\begin{bmatrix} 2 \ 1 \end{bmatrix}$)를 곱해줌으로써 복원할 수 있다.

\[\begin{bmatrix} 4.08\\2.04 \end{bmatrix}, \begin{bmatrix} 7.92\\3.96 \end{bmatrix}, \begin{bmatrix} -2.008\\-1.004 \end{bmatrix}, \begin{bmatrix} -6\\-3 \end{bmatrix} \tag{10.6}\]

이러한 과정을 더 많은 데이터를 이용해 visualization하면 아래 [그림 2]와 같이 표현할 수 있다.

[그림 2] Example of dimensionallity reduction

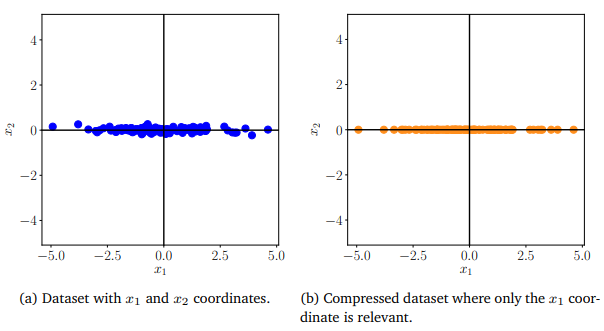
위 예제에서 살펴봤듯이 데이터를 가장 잘 표현하는 basis를 이용하여 차원을 축소하는 것이 앞으로 소개할 주성분 분석(PCA)의 원리를 이용한 것이며, 그 때의 basis (위 예제에서는 $\begin{bmatrix} 2\\1 \end{bmatrix}$)를 주성분 벡터(principal component)라고 한다.

이번 챕터에서는 이러한 주성분 분석(principal component anlaysis, PCA)의 원리와 과정에 대해서 다루고, 실제로 어떻게 적용하는 지에 대해 자세히 다룰 것이다.