방향 그래프 모델

Chapter 5 : Directed Graphical Models

8.5절에서는 조건부 독립을 표현하는 수학적 표현을 이해하고, 시각적인 그래프로 표현하는 방식에 대해 알아본다.

Edited by / 최원준 (jo0n-lab)

Conditional Independence

$\begin{equation} p(X,Y|Z)=p(X|Z)p(Y|Z) \textrm{ 이면, }\\ \end{equation}$

$\begin{align} p(X,Y|Z) &=\frac{p(X,Y,Z)}{p(Z)}=\frac{p(X|Y,Z)p(Y,Z)}{p(Z)}=p(X|Y,Z)p(Y|Z)\\ &=p(X|Z)p(Y|Z)\\ \end{align}$

$\begin{equation} \therefore p(X|Z)=p(X|Y,Z) \end{equation}$

위를 다음과 같이 축약하여 표현한다.

$\begin{equation} X\perp Y|Z,\;Y\perp X|Z \end{equation}$

즉, ‘ $X$ 와 $Y\,given\,Z$ 는 독립이다.’ 이와 같은 상황을 조건부 독립이라고 한다.

그러나 이러한, 수학적 표현 및 용어만으로는 직관적으로 이해하기 힘들다.
다음의 예시를 통해 이해해보자.

$\textrm{Fig.0}$ - 조건부 독립의 예시

명령을 내리는 상사( $C$ )와 부하직원 2명( $A,B$ )이 있다고 가정해 보자. 만약 $A$ 가 $B$ 가 앞으로 가는 것을 관찰했다고 하면, $A$ 는 $B$ 가 $C$ 로부터 명령을 전달받고 움직이고 있다고 생각할 수 있다.

이 때 $A$ 가 앞으로 갈 확률을 생각해 보자. 그 확률은 $B$ 가 앞으로 가고 있는걸 보지 못했을 때의 확률보다는 작을 것이다. (조직 사회의 특성을 생각해 보자)

$P(A_{Go}∣B_{Go})>P(A_{Go})$

이것은 $A$ 와 $B$ 가 독립이(marginal independence) 아닌 종속임을 보여준다.

$C$ 가 ‘앞으로 가!’ 라고 명령을 내린 상황에선 어떠한가?

이 경우 A 는 B 가 앞으로 가고 있는 것을 보고 있었을지라도 C 가 가라고 이미 명령했다는 사실을 알고 있기 때문에 B 가 앞으로 가고 있다는 사실과 관계없이 앞으로 가게 된다. 이 경우 B 가 앞으로 가고 있다는 사실은 상사의 명령을 전달 받은 A 입장에서 영향을 미치지 않는 정보가 된다.

이 때 다음과 같이 쓸 수 있다.

$P(A_{Go},B_{Go}|C_{Go})=P(A_{Go}∣C_{Go})P(B_{Go}∣C_{Go})$

요약하면, $A$ 와 $B$ 가 종속인 이유가 $C$ 에 모두 들어있으니, $C$ 가 전제되면 $A$ 와 $B$ 는 겹치는게 없다.

Mathematical expression to Graph

앞서 설명한 조건부 독립과 종속성을 그래프로 표현하는 방법에 대해 알아보자.

$\textrm{Fig.1}$ -

$P(A,B|C)=P(A∣C)P(B∣C)$ 의 그래프 표현

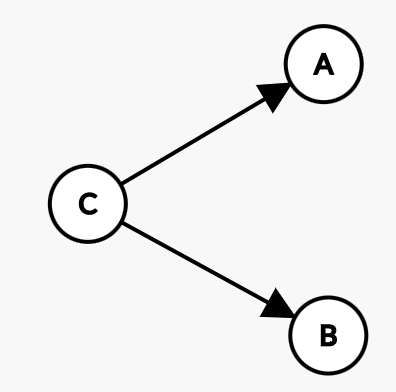
그림의 모양은 $C$ 로부터 나온 줄기(tail), $B,C$ 를 가리키는 머리(head) 로 이루어져 있다. 그리는 방법은

tail 쪽에 주어진(given : $A$ ) 노드
head 쪽에 종속된(dependent : $B,C$ ) 노드

를 이어주면 된다.

Graph to Mathematical Expression

그리는 방식에 대해 알았으니, 그래프로부터 수학적 표현을 이끌어내는 법에 대해 알아보자.

$\textrm{Fig.2 & Fig.3}$

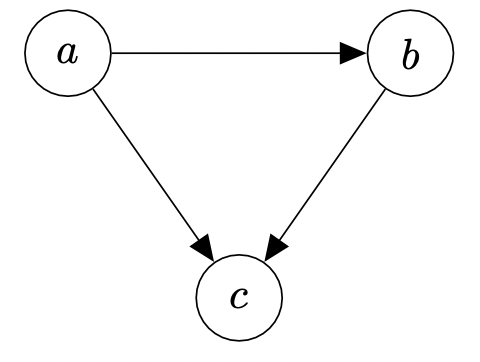
$\textrm{Fig.2}$ 의 수학적인 표현은 다음과 같다.

$\begin{equation} p(a, b, c) = p(c | a, b)p(b | a)p(a) \end{equation}$

위 표현을 이끌어내는 단계를

head의 갯수가 제일 작은 노드( $a$ )를 찾는다. (만약 비순환(acyclic) 그래프라면 0개이다.)

acyclic 이라면 완전 독립된 노드이므로 독립항( $p(a)$ )으로 곱한다.

그다음으로 head의 갯수가 작은 노드를 선택한다.

종속성 관례를 고려하여 종속항으로( $p(c | a, b)$ ) 곱한다.

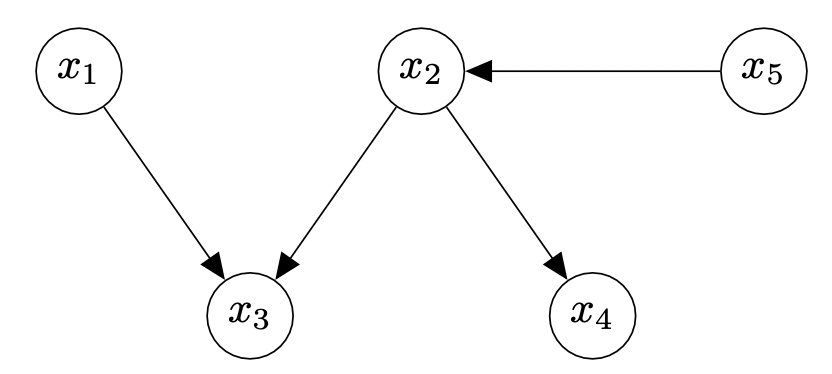
이를 $\textrm{Fig.3}$ 에 적용하면 다음과 같다.

head 갯수가 제일 작은(:0) 노드 $p(x_1)p(x_5)$
그 다음으로 갯수가 작은(:1) 노드 $p(x_1)p(x_5)p(x_2|x_5)$
(:3) 노드 $p(x_1)p(x_5)p(x_2|x_5)p(x_4|x_2)$
(:3) 노드 $p(x_1)p(x_5)p(x_2|x_5)p(x_4|x_2)p(x_3|x_1,x_2)$

따라서, $p(x_1,x_2,x_3,x_4,x_5)=p(x_1)p(x_5)p(x_2|x_5)p(x_4|x_2)p(x_3|x_1,x_2)$ 이다.

Conditional Independence in Graph

이제 그래프에서 종속성 관계를 확인하는 법을 알아보자.

$\textrm{Fig.4 & Fig.5 & Fig.6}$

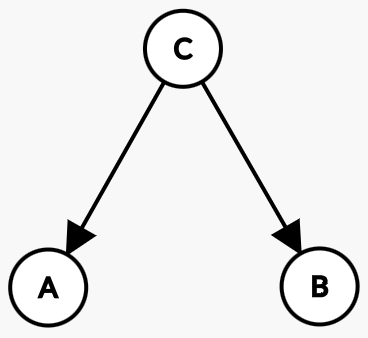
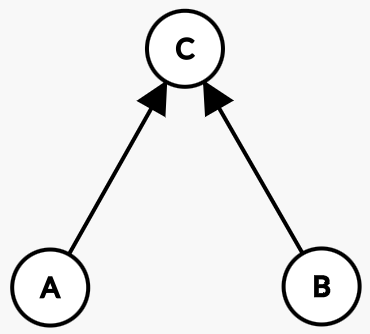
그래프에서 종속성 관계는 다음과 같은 규칙으로 판별이 가능하다.

$A$ 에서 $B$ 로 가는 경로 상

[tail, tail] 혹은 [tail, head]가 $\textrm{set} C$ 을 가리킬 때 ( $\textrm{Fig.4 & Fig.5 O}$ )
[head, head] 가 가리키는 노드가 $\textrm{set} C$ 에 포함되지 않을 때 ( $\textrm{Fig.5 X}$ )

$A \perp B|C \textrm{ 가 성립한다.}$

'When Models Meet Data' 카테고리의 다른 글