문제 공식화
Chapter 1 : Problem Formulation
선형 회귀 (Linear Regression)정의
우도함수
관측 노이즈($\epsilon$)가 필연적으로 발생하기 때문에 확률론적 접근법을 채택하고 우도 함수(likelihood function)를 사용하여 명시적으로 노이즈를 모델링할 것이다. 더 구체적으로 말하면 챕터 전체에서 가능도 함수라고도 불리는 우도 함수(likelihood function)를 이용해서 회귀에 대해 다룰 것이다.
- 우도함수(likelihood function)
우도함수를 이용한 선형회귀 정의
\[p(y|x,\theta) = \mathcal{N}(y|f(x), \sigma^2)\]여기서 입력은 $x \in R_D$ 을 만족하고 $y \in R$ 로 노이즈가 섞인 함수값이며 타겟(target)이다. 우도함수를 이용하여, x와 y의 함수적 관계를 표현한 식은 아래와 같다.
\[y = f (x) + \epsilon\]$\epsilon \sim \mathcal{N}(0,\sigma^2)$는 독립이며, 평균이 0이고 분산이 $\sigma^2$인 가우시안 분포를 따른다. 회귀의 목적은 정확한 데이터를 생산하고 일반화 시키는 $f$와 가장 가까운 혹은 비슷한 함수를 찾는 것이다. 즉, 함수를 통해 주어진 데이터를 생산할 수 있어야하고, 해당 함수는 그러한 데이터를 잘 일반화한 형태여야 된다는 것을 의미한다.
이 Chpater에서는 매개변수 모델에 중점을 둔다. 즉, 매개 변수화된 함수를 선택하고 데이터를 모델링하는 데 “적합한” 매개 변수를 찾는데에 중점을 둔다는 것이다. 당분간, 노이즈의 분산 $\sigma^2$라고 가정하고 모델 매개 변수 θ 학습학습하는데 초점을 둔다. 선형 회귀 분석에서 매개 변수 θ가 모델에 선형으로 나타나는 특수한 경우를 다루게 되는 것이다.
\[p (y|x,\theta) = \mathcal{N}(y|x^T\theta, \sigma^2) \Leftrightarrow y=x^T\theta +\epsilon, \epsilon \sim \mathcal{N}(0,\sigma^2)\]예시 1) 선형회귀의 아래와 같다.
우리가 찾는 매개변수는 $theta \in R_D$. 우변의 함수는 원점을 통과하는 직선이며, $y=x^T\theta$를 우리의 모델로 선택했다. 좌변의 우도함수(likelihood function)는 $x^T\theta$에서 $y$로 맵핑된 확률 밀도 함수이다. 불확실성의 단 하나의 원인은 관측 노이즈에서 비롯된다는 점에 유의해야한다. 관측 잡음이 없으면 x와 y 사이의 관계는 결정론적이며 Dirac Delta가 된다.
예시2) $x,θ \in R$의 경우 위 식의 우변의 선형 회귀 모형은 직선(선형 함수)를 보여주며, θ는 선의 기울기가된다. 아래 그림1은(a)는 $\theta$의 다양한 값에 대한 여러 함수를 보여준다.
그림1 CHAPTER 9 theta를 이용한 다양한 선형회귀 예시
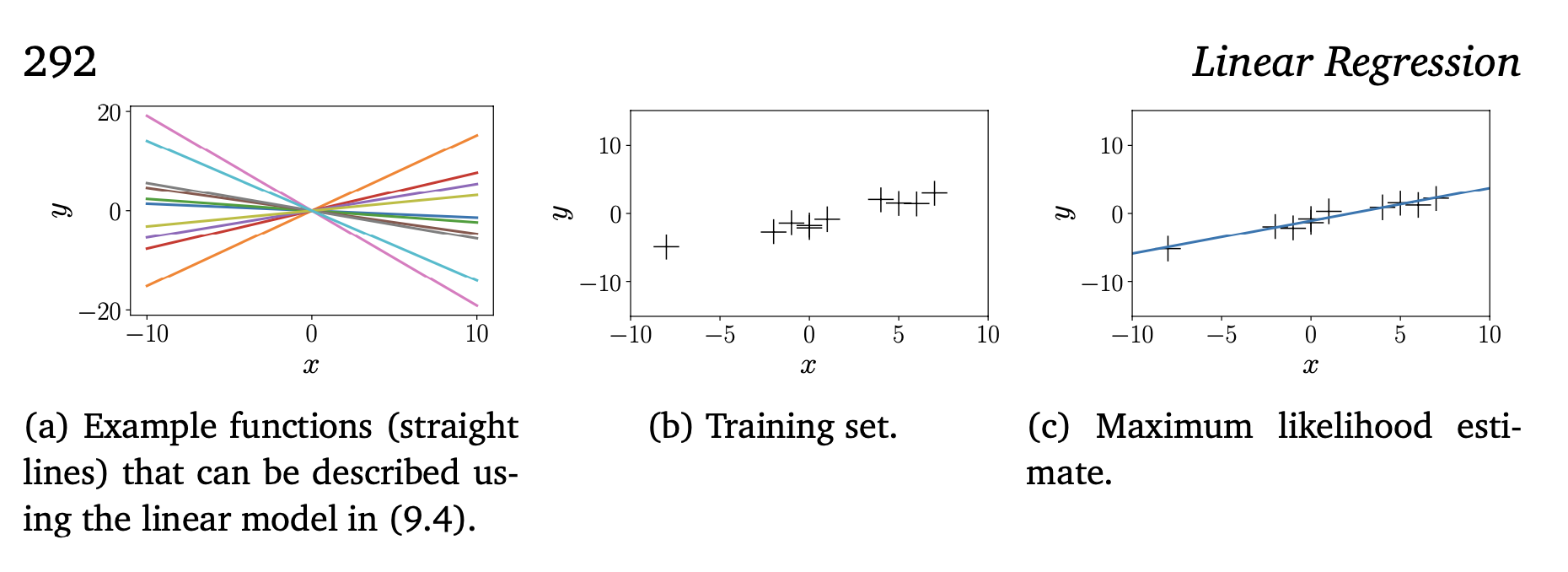
위 식에서 제시된 선형 회귀 모델은 매개 변수에서 선형일 뿐만 아니라 입력 x에서도 선형관계에 있다. 챕터에서 나중에 $y = \phi^T(x)$를 이용해 비선형 변환에 대해서도 살펴볼 것이다. 이때의 비선형 변환 $\phi$는 또한 선형 회귀 모델인데, “선형 회귀 모델”이란 “매개변수들이 선형관계에 있음”을 의미하기 때문이다. 따라서 모델은 입력 특징(features)들의 선형 조합으로 설명할 수 있다. 여기서 특징(features)는 입력 x의 $\phi(x)$의 표현식을 의미한다. 다음 소섹션에서는 좋은 매개 변수 $\theta$를 찾는 방법과 매개 변수 집합이 모델에 적합한지 평가하는 방법에 대해 자세히 설명한다. 이때에,노이즈의 분산은 $\sigma^@$으로 가정한다.