베이지안 선형 회귀
Chapter 3 : Bayesian Linear Regression
-
목차
챕터소개(Introduction)
이전 챕터에선, maximum a likelihood estimation(MLE) 또는 maximum a posterior estimation(MAP)를 통한 모델의 파라미터 $\theta$를 추정하는 linear regression model에 대해 살펴보았다.
그러나 MLE의 경우 심한 overfitting 현상을 보였으며, MAP는 이를 해결하기 위해 regularizer의 역할을 하는 prior를 고려하였지만 여전히 overfitting 현상을 보였다.
Bayesian linear regression는 예측을 진행할 때 파라미터에 대한 full posterior distribution을 사용한다. 이는 point estimate(MLE, MAP 방식)처럼 파라미터를 fit하는 대신, 가능한 파라미터 셋으로부터 mean을 계산하는 방식을 의미한다.
베이지안 선형회귀(Bayesian linear regression)
모델(Model)
베이지안 선형회귀에선 다음의 모델을 고려한다.
\[\begin{align} & prior \qquad \qquad p(\theta) = \mathcal{N}(m_0, S_0) \\ & likelihood \qquad p(y|x,\theta) = \mathcal{N}(y|\phi^T(x)\theta, \sigma^2) \\ \end{align}\]식(1)은 $\theta$ 에 관한 Gaussian prior인 $p(\theta) = \mathcal{N}(m_0, S_0)$ 이며, 이는 파라미터 벡터를 확률변수로 고려한다는 것을 알 수 있다.
사전 예측(Prior prediction)
사전 예측이란, 파라미터의 사전 분포(prior distribution)를 사용하여 모든 가능한 파라미터 셋에 대해 평균화하는 예측을 의미한다.
구체적으로 말하자면, input $ x_* $에 대한 예측을 진행할 때 아래 식(3)과 같이 파라미터에 대해 적분을 수행하며, 이는 prior distribution $p(\theta)$를 고려하여 모든 파라미터 $\theta$에 대해 $ y_* | x_* , \theta $ 의 평균을 예측한다고 해석할 수 있다.
Prior distribution을 사용한 예측인 사전 예측은 training data 필요없이 input $x_*$ 만을 필요로 한다.
식 (3) 에 앞서 본 식 (1) 인 $p(\theta) = \mathcal{N}(m_0, S_0)$ 를 고려하여 다음과 같은 예측 분포를 얻을 수 있다.
\[\begin{align} p(y_*|x_*) = \mathcal{N}(\phi^T(x_*)m_0, \phi^T(x_*)S_0\phi(x_*) + \sigma^2) \end{align}\]위 식 (4) 에서 $ \phi^T( x_* ) S_0 {\phi( x_* )} $ 텀은 파라미터 $ \theta $의 불확실성으로부터 비롯된 예측 variance를 의미하며, $\sigma^2$ 텀은 measurement noise의 불확실성으로부터 비롯된 variance를 의미한다.
만약 우리가 noise-free 값에 대해 예측을 진행하고 싶다면 아래의 식을 사용하여 구할 수 있다.
\[\begin{align} p(f(x_*)) = \mathcal{N}(\phi^T(x_*)m_0, \phi^T(x_*)S_0\phi(x_*)) \end{align}\]이는 noise variance인 $\sigma^2$이 제거되었다는 점에서 차이가 있다.
Prior over functions
함수 샘플은 파라미터 벡터 $\theta_i ~ p(\theta)$를 샘플링하여 얻을 수 있으며, $f_i(\cdot) = \theta_i^T\phi(\cdot)$ 을 통해 계산할 수 있다.
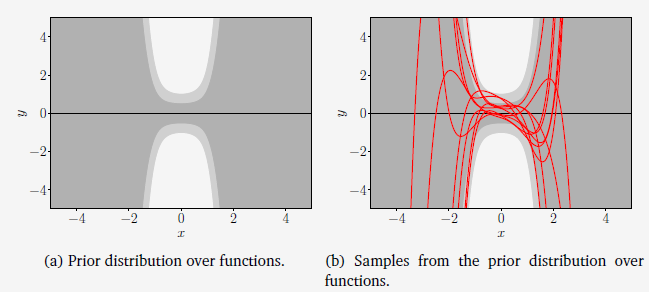
예시1)
5차원의 다항식에 관한 베이지안 선형 회귀 문제를 다룬다고 가정하자.
이때 prior $p(\theta) = \mathcal{N}(0, {1 \over 4}I)$ 라고 하면, parameter prior에 의해 [그림 1.(a)] 처럼 prior distribution over function을 시각화할 수 있다. (그늘진 영역: 67% confidence bound, 밝은 회색 영역: 95% confidence bound를 의미한다.)
[그림 1.(b)] 는 parameter prior로부터 추출한 샘플을 사용하여 계산한 함수들을 시각화한 것이다.
그림1 Prior over functions
지금까지 파라미터 prior인 $p(\theta)$를 사용한 예측 방법에 대해 살펴보았다. 그러나 우리가 training data $\mathcal{X}, \mathcal{Y}$ 가 주어졌을 때의 파라미터 posterior를 가지고 있다면, 식 (3) 와 같은 원리로 예측과 추론을 진행할 수 있다. 단지 prior $p(\theta)$ 대신 posterior $p(\theta|\mathcal{X},
\mathcal{Y})$를 사용하면 된다. 이러한 예측을 posterior prediction이라 하는데, 이전에 posterior distribution에 대해 먼저 알아보도록 한다.
사후 분포(Posterior distribution)
training dataset인 input $x_n \in \mathbb{R}^D$ 와 그에 상응하는 observation $y_n \in \mathbb{R}, n = 1,…,N$이 주어졌을 때, Bayes’ theorem을 통한 파라미터의 posterior는 다음과 같이 계산한다.
\[\begin{align} p(\theta|\mathcal{X}, \mathcal{Y}) = {p(\mathcal{Y}| \mathcal{X}, \theta) p(\theta) \over p(\mathcal{Y}| \mathcal{X})} \end{align}\]이때 $\mathcal{X}$는 training input 집합을 의미하고, $\mathcal{Y}$는 training target의 집합을 의미한다.
위 식에서 $p(\mathcal{Y}|\mathcal{X},\theta)$ 는 likelihood를, $p(\theta)$는 parameter prior를, 마지막으로 $p(\mathcal{Y}|\mathcal{X})$는 marginal likelihood/evidence 이다.
이 때, Marginal likelihood/evidence는 다음과 같이 구한다.
marginal likelihood/evidence는 파라미터 $\theta$에 독립적이며, 적분을 통해 1이 된다는 점을 통해 식 (6) posterior의 값을 normalization 해주는 역할을 수행한다.
식 (1), (2) 의 모델을 통해 식 (6) 인 posterior distribution은 다음과 같이 구할 수 있다.
\[\begin{align} p(\theta|\mathcal{X}, \mathcal{Y}) = \mathcal{N}(\theta|m_N, S_N) \\ S_N = (S_0^(-1) + \sigma^(-2)\Phi^T\Phi)^(-1) \\ m_N = S_N(S_0^(-1)m_0 + \sigma^(-2)\Phi^Ty) \\ \end{align}\]위 식의 subscript $N$은 training set의 size를 의미한다. (위 식에 대한 증명은 생략한다.)
사후 예측(Posterior prediction)
식 (3) 에서 parameter prior $p(\theta)$ 를 사용하여 test input $ x_* $에 대한 $ y_* $ 의 예측 분포를 계산할 수 있었다. Prior와 posterior 둘다 Gaussian 분포라는 점에서, parameter posterior $p(\theta|\mathcal{X}, \mathcal{Y})$를 가지고 예측하는 방법(사후 예측)은 사전 예측과 근본적으로 다르지 않다.
따라서 posterior predictive distribution은 다음과 같이 구할 수 있다.
$\phi^T( x_* ) S_N \phi( x_* )$ 텀은 파라미터 $\theta$ 에 관한 posterior uncertainty를 나타낸다. $S_N$은 $\Phi$을 통한 training input에 의존한다. Prediction mean인 $phi^T( x_* )m_N$ 은 MAP를 통해 얻은 $\theta_(MAP)$를 사용하여 예측한 결과와 동일하다.
Marginal Likelihood와 Posterior Predictive Distribution 차이
식 (11) 은 $\mathbb{E}_(\theta|\mathcal{X},\mathcal{Y})[p(y_*|x_*,\theta)]$ 로 바꿔쓸 수 있으며, 이는 parameter posterior $p(\theta|\mathcal{X},\mathcal{Y})$에 관한 기댓값을 의미한다. 이는 식 (7)인 marginal likelihoood와 닮은 것을 확인할 수 있지만, 다음과 같은 차이점을 가지고 있다. 1. Marginal likelihood는 test target $y_*$ 이 아닌, training target $y$를 예측한다. 2. Marginal likelihood는 parameter posterior가 아닌 parameter prior에 관해 평균화한다.Posterior over Functions
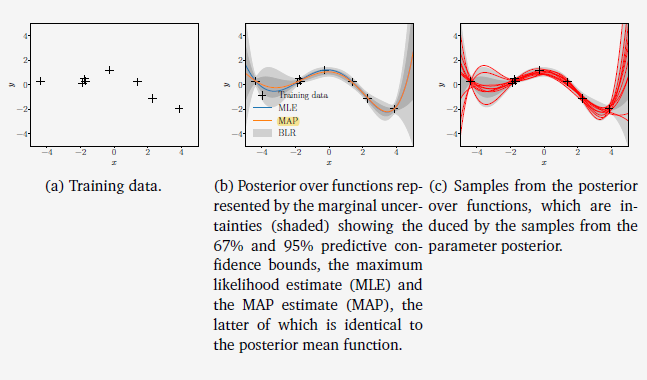
예시2)
앞서 본 예시 1 처럼 5차원 다항식의 베이지안 선형 회귀 문제를 다룬다고 하자. [그림 1] 은 prior $p(\theta) = \mathcal{N}(0, {1 \over 4}I)$일 때의 parameter prior와 샘플 함수로 인한 prior over function을 시각화한 그림이다. [그림 2] 는 베이지안 선형 회귀를 통해 얻은 posterior over function의 결과를 보여준다. [그림 2.(a)] 는 우리가 고려할 training dataset 을 나타낸다. [그림 2.(b)] 는 training dataset을 사용하여 MLE, MAP 추정과 posterior 예측의 결과를 보여준다. 이때 MAP 추정은 베이지안 선형 회귀를 통한 posterior mean function에 상응하는 것을 확인할 수 있다. [그림 2.(c)] 는 parameter posterior 에서 샘플링하여 계산한 함수를 보여준다.
그림2 Posterior over Functions
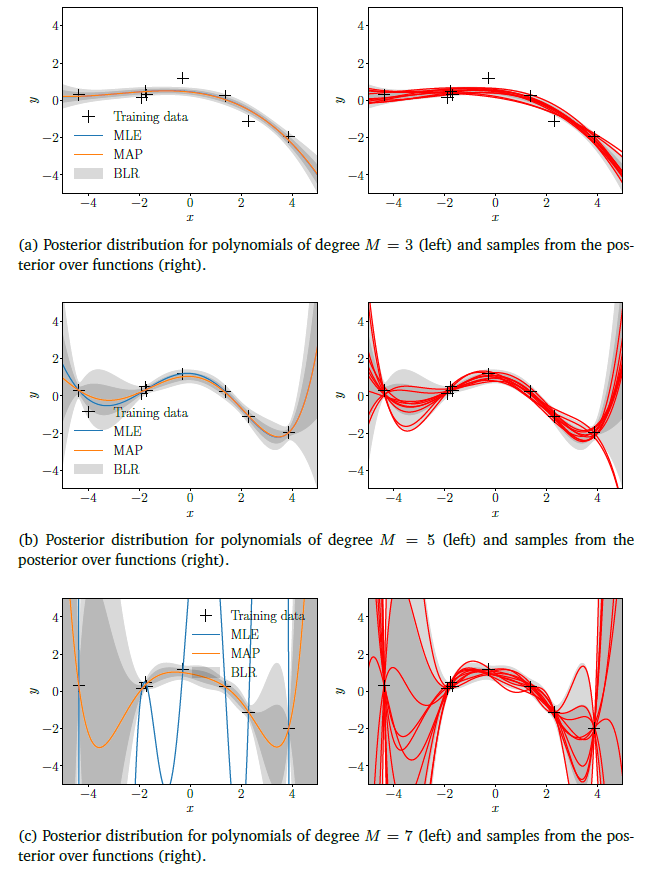
[그림 3] 은 parameter posterior에 의한 posterior distribution을 보여준다. 각각 다른 M차 다항식에 대해, 왼쪽 그림들은 MLE, MAP, 그리고 베이지안 선형 회귀를 통해 얻은 67%, 95% predictive confidence bound를 나타낸다. 오른쪽 그림들은 posterior over function으로부터 샘플들을 보여준다.[그림 3.(a)]
Low-order polynomial에 대해선 parameter posterior가 크게 달라지는 것을 허용하지 않으며, 샘플링한 함수들도 거의 동일한 것을 확인할수 있다.[그림 3.(b)], [그림 3.(c)]
고차원 다항식으로 갈수록, posterior에 의해 크게 구속되지 않으며, 이는 샘플링 함수들이 시각적으로 분리된다는 점을 통해 알 수 있다. 또한 uncertainty가 어떻게 증가하는지 boundary를 통해 알 수 있다.
비록 7차원 다항식에서 MAP 추정이 적당한 fit을 보여주지만, 베이지안 선형회귀 모델은 이에 추가적으로 posterior uncertainty 또한 보여주고 있다. 이러한 정보는 잘못된 결정을 할 때 중요한 결과를 불러일으키는 decision-making system에서 prediction을 할 때 중요하게 사용될 수 있다. (reinforcement learning 또는 robotics)
그림3 베이지안 선형회귀