경사하강법을 통한 최적화

Chapter 1 : Optimization Using Gradient Descent

Edited by / 임수형 (sulogc)

경사하강법

경사하강법은 1차 최적화 알고리즘이다. 5.1 에서 경사(gradient)는 가장 가파른 오르막을 가리키는 것을 배웠다. 지역 최소값을 구하기 위해서는 경사의 반대로 가야한다. 목적함수 f(x) = c 일때, x의 집합, 등고선을 생각해보자. 여기서 경사는 등고선(값이 유지되는 선)에 수직을 가리킨다.

다음 $ f : \mathbb{R}^d \rightarrow \mathbb{R} $ 에서 정의되는 실함수의 최소값을 찾는 문제를 보자. $f$ 는 미분가능하고, 닫힌 형식의 해석적 해를 찾을 수 없다고 하자.

\[\begin{align} \min\limits_{x} f(x) \end{align}\]

여기서 f가 다변수 함수(x : vector)일 때, $f$ 가 $x_0$ 에서 가장 빠르게 줄어드는 방향인 경사는 $ -((\nabla f)(x_0))^\top $ 이고, step크기 $\gamma$ 를 통해 다음과 같이 업데이트 할 수 있다.

\[\begin{align} x_1 = x_0 - \gamma((\nabla f)(x_0))^\top \end{align}\]

이를 일반화 하면 다음과 같이 표현 가능하다.

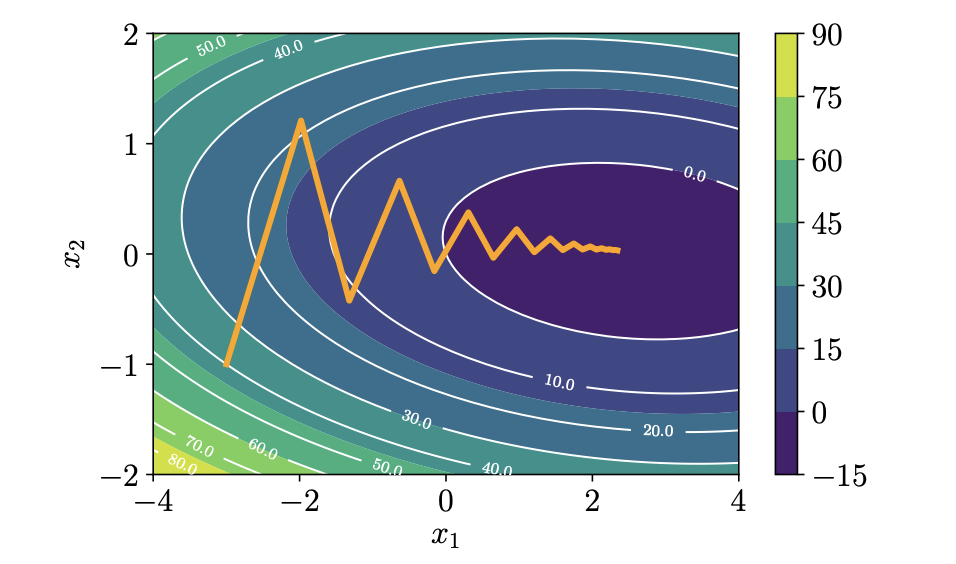
\[\begin{align} x_{i+1} = x_i - \gamma _i ((\nabla f)(x_i))^\top \end{align}\]

적절한 $\gamma$ 가 설정되고, 알고리즘 반복시 점점 줄어드므로, $ f(x_0) \geqslant f(x_1) \geqslant … $ 업데이트 되는 $x$ 에 의한 $f(x)$ 의 값은 지역 최소값에 수렴하게 된다. 그러나 목적함수의 형태가 매우 평평한 계곡과 같은 경우, 경사 하강시 기울기의 방향이 지그재그로 표현되어 점근적인 수렴이 다른 알고리즘보다 느리다는 문제가 있다.

그림1 Zigzags in 2D quadratic surface

Step의 크기

step의 크기 설정은 매우 중요하다. 너무 작으면, 학습이 매우 느릴 것이고, 크면 Overshoot하고 발산해 버릴 수도있다. 모멘텀에 대해서 소개하기 전에 적응형 경사 방법을 알아보자. 적응형 경사(AdaGrad)는 각 반복마다 함수의 로컬 속성에 따라 step 크기를 조정하는데, 다음 두 가지 간단한 휴리스틱을 사용한다.

step 이후 함수값이 증가할 경우, step크기가 매우 크다는 것 이므로, step을 취소하고 step크기를 감소시킨다.
함수 값이 감소할 경우, 더 큰 step이 가능했으므로, step크기를 키운다.

이 휴리스틱에서 step을 취소하는 것이 자원 낭비처럼 보여도, 단조 수렴을 보장한다.

조건수와 선조건자

모멘텀

그림1 에서 보듯 최적화의 대상이 되는 함수 표면의 곡률이 poorly scaled된 경우, 경사하강의 수렴은 매우 느리게 진행된다. 계곡의 벽면을 건너뛰며 진행되는 양상으로 작은 step을 가져가게 된다. 여기서 약간의 메모리를 사용해서 수렴에 도움을 줄 수 있다.

모멘텀을 이용한 경사하강법은 이전 반복에서 무슨 일이 일어났는지 기억하는 항을 추가하는 방법이다. 이 항은 진동을 완화하고 업데이트를 부드럽게 하는데, 마치 무거운 공을 사용해 방향을 어느정도 유지하는 것으로 이해 할 수 있다.

이전 업데이트 시 $x$ 의 변화량을 다음 업데이트에 일정비율로 사용하는 방법으로 다음과 같이 나타낼 수 있다. $ \alpha \in [0, 1] $ 에 대해

\[\begin{align} x_{i+1} = x_i - \gamma _i ((\nabla f)(x_i))^\top + \alpha \Delta x_i \end{align}\] \[\begin{align} \Delta x_i &= x_i - x_{i-1} & \\ &= \alpha \Delta x_{i-1} - \gamma _{i-1} ((\nabla f)(x_{i-1}))^\top \end{align}\]

정확한 기울기 대신 근사적인 기울기를 구할 수 있지만, 기울기의 noise를 평균화 하기때문에 유용하다.

확률적 경사하강

경사(gradient)를 계산하는 것은 매우 비용이 많이 든다. 그러나, 확률적 경사 하강을 통해 저렴한 근사적 기울기를 구하는 것이 가능하다. 확률적 경사하강(SGD)은 목적함수가 미분가능한 함수들의 합으로 표현되고, 이를 최소화하는 경사하강법에 확률적 근사를하는 방법이다. 여기서, 근사된 경사(gradient)의 확률분포를 제한 할 수 있어서 SGD가 수렴하는 것을 보장할 수 있다.

머신러닝에서, n개의 데이터에 대해 목적함수는 각 loss의 합으로 표현된다. $ \theta $ 를 모델의 파라미터 벡터라고 하면,

\[\begin{align} L(\theta) = \sum_{n=1}^N L_n(\theta) \end{align}\]

$L$ 을 최소화하는 $ \theta $ 를 찾는 것이 목표이다. 회귀 문제에서 손실함수인 음의 로그 우도를 예시로 보자. $ x_n \in \mathbb{R}^D $ 가 학습 인풋, $ y_n $ 가 타겟, 그리고 $ \theta $ 가 회귀 모형의 파라미터일 때,

\[\begin{align} L(\theta) = - \sum_{n=1}^N {\log p (y_n \mid x_n, \theta) } \end{align}\]

기존에 소개한 경사하강법은, “batch” 최적화 방법으로, 파라미터 학습에 학습 데이터셋 전체를 사용한다. 학습 데이터의 양이 방대하고, 복잡한 계산만 있을 경우, 모든 손실함수에 대한 경사(gradient)를 계산하기엔 비용이 매우 크다.

\[\begin{align} \theta _{i+1} &= \theta _i -\gamma(\nabla L(\theta _i))^\top & \\ &= \theta _i - \gamma \sum_{n=1}^N {(\nabla L_n(\theta _i))^\top} \end{align}\]

위와 같이 경사 하강 알고리즘에서 파라미터가 업데이트 될 때, $ \nabla L_n(\theta _i) $ 항을 보자. $ L_n $ 의 크기를 줄여서 계산 비용을 줄일 수 있다. 미니-배치 경사하강법 은 $ n = 1, …, N $ 에 대해, 각 반복 시 랜덤한 $ L_n $ 항을 선택하여 파라미터를 업데이트한다.

데이터의 하위 집합을 선택하는 것은 실제 경사(gradient)의 편향되지 않은 추정치들을 사용하는 것으로 해석 할 수 있다. 즉, 특정 데이터에 대한 의존도를 낮추는 것으로 볼 수 있다.

경사(gradient)의 근사치

왜 경사에 대해 근사치를 쓸까? CPU, GPU 메모리 크기, 계산 시간의 한계에 의해 실제 구현의 제약이 있다. 또한 표본 평균을 계산하여 사용하듯, 일반화된 경사를 사용하는 것으로도 생각할 수 있다.

미니 배치 사이즈간 trade-off가 있다. 배치 사이즈가 클 경우, 파라미터 업데이트의 변동성을 줄이고, 분산의 감소로 안정적으로 수렴 할 수 있지만, 계산 비용이 높다. 배치 사이즈가 작을 경우, 빠르게 계산 가능하며 근사치 이기 때문에 발생한 noise에 의해 지역 최소값에서 벗어날 수 있다.

모델 학습시, 파라미터들을 목적함수가 최소가 되도록 특정 학습데이터를 이용해 최적화를 진행하지만, 전반적인 목표는 일반화 성능 향상 이므로 미니 배치를 사용한 경사 근사치가 자주 사용된다.

'연속 최적화' 카테고리의 다른 글