가우시안 분포
Chapter 5 : Gaussian Distribution
Edited by / 유민정 (Minjeong-Yoo)
-
목차
가우시안 분포
가우시안 분포(Gaussian distribution)은 continuous-valued variables 에 대해 가장 널리 알려진 확률분포이다. 이는 normal distribution 이라고도 불린다. 가우시안 분포의 중요성은 계산적인 측면에서 용이한 특성을 많이 가지고 있다는 점에서 비롯되었다.
머신러닝에서도 마찬가지로 Gaussian processes, variational inference, 강화학습 등에서 가우시안 분포를 많이 사용한다. 뿐만 아니라 signal processing(e.g., Kalman filter), control (e.g.,
linear quadratic regulator) 등 여러 분야에 걸쳐 사용되고 있다.
단일 변수 가우시안 분포(univariate Gaussian distribution)
Univariate random variable에 대해 가우시안 분포는 다음과 같은 밀도함수를 갖는다.
\[\begin{align} p(x|\mu,\sigma^2) = {1 \over \sqrt{2\pi\sigma^2}}exp(-{(x-\mu)^2 \over 2\sigma^2}) \end{align}\]다변수 가우시안 분포(multivariate Gaussian distribution)
Multivariate Gaussian distribution은 mean vector $\mu$와 covariance matrix $\sum$에 의해 특성화되며, 식은 다음과 같다.
\[\begin{align} p(x|\mu,\sum) = (2\pi)^{-{D\over 2}}|\sum|^{-{1 \over 2}}exp(-{1 \over 2}(x - \mu)^T\sum^{-1}(x - \mu)) \end{align}\]여기서 $x \in \mathbb{R}^D$ 이다. $p(x) = \mathcal{N}(x|\mu, \sum)$ 또는 $X \sim \mathcal{N}(\mu, \sum)$로 쓴다.
### **그림1** 가우시안 분포
{: .no_toc .text-delta }
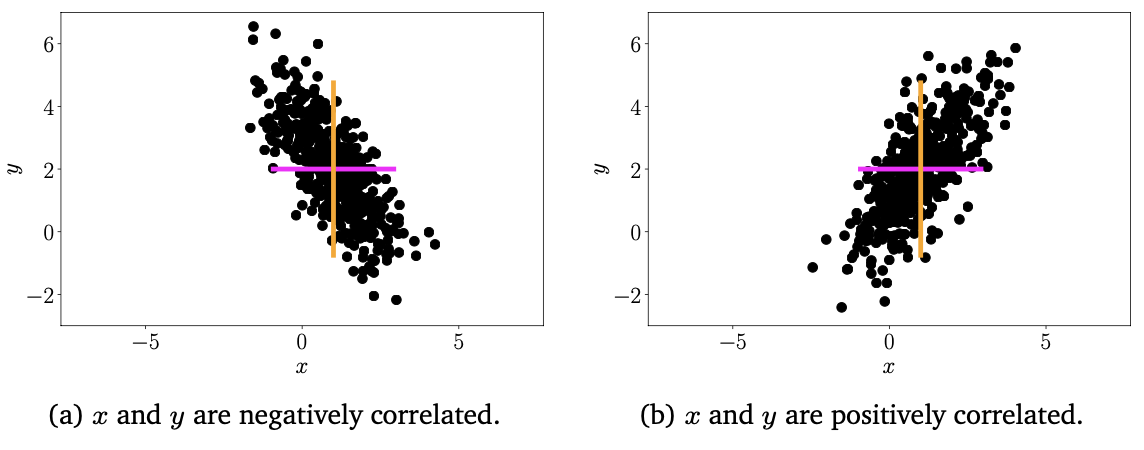
위 그림은 각각 해당하는 sample에 대한 univariate gaussian과 bivariate gaussian을 보여준다.
평균이 0이고 identity covariance의 특성($\mu = 0, \sum = I$)을 갖는 가우시안 분포의 경우, standard normal distribution이라고 한다.
가우시안 분포는 marginal distribution와 conditional distribution에서 closed-form으로 표현할 수 있어 statistical estimation과 machine learning에서 널리 사용된다. 가우시안 분포는 mean와 covariance 만으로 완벽히 표현할 수 있기 때문에 확률변수의 mean와 covariance에 transformation을 적용하여 transformed distribution을 얻을 수 있다.
Marginals and Conditionals of Gaussians are Gaussians
일반적인 multivariate random variable 에서의 marginalization과 conditioning 에 대해 다뤄본다.
X와 Y를 차원이 다른 두 개의 multivariate random variable 이라 가정한다. 확률의 sum rule과 conditioning을 다루기 위해 states $[x,y]^T $항의 가우시안 분포를 아래와 같이 표현한다.
여기서 $\sum_{xx} = Cov[x,x], \sum_{yy} = Cov[y,y]$는 각각 x와 y의 marginal covariance matrix 이다. $\sum_{xy} = Cov[x,y]는 x와 y의 cross-covariance matrix 이다.
Conditioning
Conditional distribution $p(x|y)$ 또한 가우시안 분포를 보이며, 다음과 같이 주어진다.
\[\begin{aligned} p(x,y) &= \mathcal{N}(\mu_{x|y}, \sum\nolimits_{x|y}) \end{aligned}\] \[\begin{align} \mu_{x|y} &= \mu_x + \sum\nolimits_{xy}\sum\nolimits_{yy}^T(y-\mu_y) \end{align}\] \[\begin{align} \sum\nolimits_{x|y} &= \sum\nolimits_{xx} - \sum\nolimits_{xy}\sum\nolimits_{yy}^{-1}\sum\nolimits_{yx} \end{align}\]Marginalization
Joint gaussian distribution $p(x,y)$의 marginal distribution $p(x) 또한 가우시안 분포를 보이며 sum rule을 적용하여 다음과 같이 계산한다.
\[\begin{align} p(x) = \int p(x,y)dy = \mathcal{N}(x|\mu_x, \sum\nolimits_{xx}) \end{align}\]가우시안 분포 곱(Product of Gaussian Densities)
Linear regression(chapter 9)에서, 우리는 Gaussian likelihood를 계산할 필요가 있다. 또한 gaussian prior에 대한 가정을 바탕으로, 우리는 Bayes’ theorem을 적용하여 likelihood와 prior의 gaussian density 곱의 결과인 posterior를 계산한다. 이는 두 gaussian 분포의 곱인 $\mathcal{N}(x|a, A)\mathcal{N}(x|b, B)$와 같으며, $c \in \mathbb{R}$로 스케일된 가우시안 분포 $c_3\mathcal{N}(x|c_2, c_1) $이다.
\[\begin{align} c_1 = (A^{-1} + B^{-1})^{-1} \\ \end{align}\] \[\begin{align} c_2 = c1(A^{-1}a + B^{-1}b) \end{align}\] \[\begin{align} c_3 = (2\pi)^{-{D \over 2}}{A + B}^{-{1 \over 2}}exp(-{1 \over 2}(a-b)^T(A+B)^{-1}(a-b)) \end{align}\]여기서 scailing constant $c_3$는 “inflated” covariance matrix $A+B$가 있는 a 혹은 b의 가우시안 밀도의 형식으로 다음과 같이 표현할 수 있다.
\[\begin{align} i.e., c_3 = \mathcal{N}(a|b, A+B) = \mathcal{N}(b|a, A+B) \end{align}\]| a와 b는 확률변수는 아니지만, 표기의 편의를 위해 $\mathcal{N}(x | m,S)를 사용하여 가우시안 밀도의 형태로 표현하기도 한다. |
합과 선형변환(Sums and Linear Transformations)
X, Y 가 독립적인 가우시안 확률변수이고 $p(x)=\mathcal{N}(x|\mu_x, \sum_x)$, $p(y)=\mathcal{N}(y|\mu_y, \sum_y)$ 이면,
$x+y$ 또한 가우시안 분포로 다음과 같이 정의한다.
이러한 특성은 확률변수에 작용하는 i.i.d.(independent identically distributed) 가우시안 노이즈를 고려할 때 중요한 특성이다.
예시1)
Expectation은 linear operation이므로, 독립적인 가우시안 확률변수들의 weighted sum 은 다음과 같이 얻을 수 있다. \(\begin{align} p(ax+by) = \mathcal{N}(a\mu_x+b\mu_y, a^2\sum\nolimits_x+b^2\sum\nolimits_y) \end{align}\)
식(11)
p(x+y)가 가우시안 분포라는 점과 mean와 covariance matrix의 값은 아래의 식을 통해서 알 수 있다.state $x,y \in \mathbb{R}^D$를 갖는 확률변수 X, Y 가 있을 때 다음 연산이 성립한다. $$ \mathbb{E}[x+y] = \mathbb{E}[x] + \mathbb{E}[y] \\ \mathbb{E}[x-y] = \mathbb{E}[x] - \mathbb{E}[y] \\ \mathbb{V}[x+y] = \mathbb{V}[x] + \mathbb{V}[y] + Cov[x,y] + Cov[y,x] \\ \mathbb{V}[x-y] = \mathbb{V}[x] + \mathbb{V}[y] - Cov[x,y] - Cov[y,x] $$
i.i.d.(independent identically distributed)
영어 뜻 그대로 확률변수가 여러 개 있을 때, 상호독립적이고 모두 동일한 확률분포를 가지고 있으면 iid 하다고 정의한다.두 가우시안 분포의 혼합(Mixture of two gaussian densities)
확률 변수 x 는 두 density $p_1(x)$ $p_2(x)$의 조합과 가중치 $\alpha$를 통해 얻어진다. 이 정의는 multivariate random variable의 경우에도 적용되는데, 이는 기댓값의 선형성이 여전히 만족하기 때문이다.
두 univariate gaussian densities의 조합은 다음과 같다.
\[\begin{align} p(x) = \alpha p_1(x) + (1 - \alpha)p_2(x) \end{align}\]여기서 스칼라 $0 < \alpha <1 $은 mixture weight, $p_1(x), p_2(x)$는 서로 다른 파라미터를 갖는 univariate gaussian density 이다. Mixture density $p(x)$의 평균은 각 확률변수의 평균의 weighted sum의 형태로 주어진다.
\[\begin{align} \mathbb{E}[x] = \alpha \mu_1 + (1 - \alpha) \mu_2 \end{align}\]Mixture density $p(x)의 variance는 다음과 같다.
\[\begin{align} \mathbb{V}[x] = [\alpha \sigma_1^2 + (1 - \alpha) \sigma_2^2] + ([\alpha \mu_1^2 + (1 - \alpha) \mu_2^2] - [\alpha \mu_1 + (1 - \alpha) \mu_2]^2) \end{align}\]참고
위 유도는 어떠한 density 에 대해서도 성립하지만, 가우스 분포만이 mean과 variance 만으로 완전히 결정되기 때문에 density의 혼합이 closed form으로 결정된다.
가우시안 확률변수의 선형변환(linear tranformation of Gaussian random variable)
Bivariate standard gaussian random variable X에 linear transformation $Ax$를 적용한 예를 고려해보면(예제 6.17), 그 결과는 zero mean에 covariance $AA^T$를 갖는 가우시안 확률변수가 된다. 여기에 constant vector $\mu$ 를 더한다면, 확률변수 $x+\mu$는 variance에는 영향을 주지 않으면서 mean $\mu$와 identity covariance의 특성을 가질 것이다.
따라서 가우시안 확률변수에 어느 linear/affine tranformation을 수행하더라도 가우시안 분포이다.
$X \sim \mathcal{N}(\mu, \sum)$인 가우시안 확률변수와 적절한 형태의 $A$에 대해, Y는 $x$가 변환된 $y = Ax 의 확률변수라 둔다. 기댓값이 linear operator임을 통해 $y$의 mean을 계산하면 다음과 같다.
\[\begin{align} \mathbb{E}[y] = \mathbb{E}[Ax] = A\mathbb{E}[x] = A\mu \end{align}\]이와 비슷하게 y의 variance를 계산하면 다음과 같다.
\[\begin{align} \mathbb{V}[y] = \mathbb{V}[Ax] = A\mathbb{V}[x]A^T = A\sum A^T \end{align}\]이는 확률변수 $y$가 다음의 분포를 따른다는 것을 의미한다.
\[\begin{align} p(y) = \mathcal{N}(y|A\mu, A\sum A^T) \end{align}\]가우시안 확률변수의 역변환(reverse tranformation)
이제 reverse tranformation에 대해 생각해본다. 즉, 확률변수가 다른 확률변수의 linear tranformation으로 이루어진 mean을 갖는 경우를 말한다. Full rank matrix $A \in \mathbb{R}^{M \times N}, M \geq N$ 에 대해, $Ax$를 mean으로 갖는 $y \in \mathbb{R}^M $확률변수라 가정하면,
\[\begin{align} p(y) = \mathbb{N}(y|Ax, \sum) \end{align}\]이에 해당하는 확률분포 $p(x)는 무엇일까? $A$가 invertible하다면, $x = A^-1 y로 쓰고 이를 적용할 수 있을 것이다. 그러나 대부분 $A$는 invertible 하지않아 pseudo-inverse를 사용한다. 이는 양변에 $A^T$을 곱하고, $A^T A$의 역행렬을 구하는 것이다. 이는 symmetric, positive definite 하다.
\[\begin{align} y = Ax \leftrightarrow (A^T A)^{-1} A^T y = x \end{align}\]따라서 $x$는 $y$의 선형변환이며, 아래와 같은 식을 얻을 수 있다.
\[\begin{align} p(x) = \mathbb{N}(x|(A^T A)^{-1} A^T y, \ (A^T A)^{-1} A^T \sum A(A^T A)^{-1}) \end{align}\]다변수 가우스 분포의 표본 추출(Sampling from Multivariate Gaussian Distributions)
multivariate gaussian의 경우, random samplling은 3단계로 구성된다.
- [0, 1] 사이의 균일분포의 sample을 제공하는 pseudo-random number
- univariate gaussian 으로부터 sample을 얻기 위한 Box-Muller transform와 같은 non-linear transformation 사용
- multivariate standard normal $\mathbb{N}(0,I)$ 로부터 sample을 얻기 위해 이러한 sample을 대조
mean이 nonzero 이고 covariance가 identity matrix가 아닌 일반적인 multivariate gaussian 의 경우, 가우시안 확률변수의 linear transformation의 성질을 이용한다. mean $\mu$, covariance matrix $\sum$ 를 갖는 multivariate gaussian distribution으로부터 sample $x_i, i = 1, …, n 을 생성한다고 가정한다. 그러면 multivariate standard normal $\mathbb{N}(0, I)로부터 sample을 생성하여 이를 구성할 것이다.
multivariate normal $\mathbb{N}(\mu, \sum)$ 으로부터 sample을 얻기 위해, 가우시안 확률변수의 linear transformation 의 성질을 이용할 수 있다. 만약 $x \sim \mathbb{N}(0, I) 이라면, $y = Ax$ 이고, 이는 mean $\mu 와 covariance matrix $AA^T = \sum$ 을 갖는 가우시안 분포임을 알 수 있다. $A$를 구하기 위한 편리한 방법 중 하나는 covariance matrix $\sum = AA^T$ 의 Cholesky decomposition을 사용하는 것이다. 이는 $A$가 삼각행렬이라는 것을 통해 효율적인 연산을 가능하게 한다.
'확률 분포' 카테고리의 다른 글
```