행렬
Chapter 2 : Matrices
-
목차
행렬은 선형대수에서 중심적인 역할을 한다.
선형 방정식을 간결하게 표현하는 데에도 사용되며, Chapter 7 에서는 뒷부분에서는 선형 변환의 역할을 하기도 한다.
자세한 내용은 Chapter 4 에서 다룰 것이기에 간단하게만 살펴보도록 하겠다.
행렬의 정의
실수 행렬 $(m, n)$ $A$ 는 $m$개의 행(rows)과 $n$개의 열(columns)로 이루어지고, 다음과 같이 표현된다.
\[A = \begin{bmatrix} a_{11} & a_{12} & \cdots &a_{1n}\\a_{21} & a_{22} & \cdots & a_{2n}\\\vdots & \vdots & & \vdots \\a_{m1} & a_{m2} & \cdots & a_{mn}\\ \end{bmatrix} ,\quad a_{ij} \in \mathbb{R}.\]단, 이 때 $m, n \in \mathbb{N}$ 가 만족해야한다. 그리고, 행렬 $A$ 의 요소의 개수는 $m \times n$ 개 이다.
특별히 $(1, n)$ 행렬과 $(m, 1)$ 행렬을 각각 행(rows), 열(columns)이라고 하는데,
이렇게 특별한 행렬을 벡터 행렬(row/column vectors)이라고 한다.
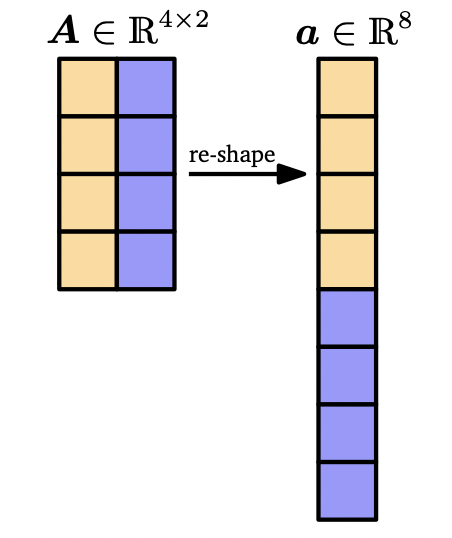
그리고 그림4 의 행렬 $A \in R^{m \times n}$ 는 모든 요소를 이어 붙인 벡터 $a \in R^{mn}$ 와 같은 표현이라는 점도 알아두자.
( $R^{m \times n}$ 는 실수공간에 있는 $(m, n)$ 행렬이다. )
그림4 행렬 A의 벡터화
C = np.einsum(’il, lj’, A, B)
행렬의 계산
행렬 $A \in \mathbb{R}^{m \times n} $ 와 $B \in \mathbb{R}^{m \times n} $ 의 합은 요소별(element-wise)로 이루어지며 다음과 같이 정의된다.
\[A + B := \begin{bmatrix} a_{11} + b_{11} & \cdots & a_{1n} + b_{1n}\\\vdots & & \vdots \\a_{m1} + b_{m1} & \cdots & a_{mn} + b_{mn}\\ \end{bmatrix} \in \mathbb{R}^{m \times n}\]행렬 $A \in \mathbb{R}^{m \times n}$ 와 $B \in \mathbb{R}^{n \times k}$ 의 곱은 $ A \cdot B = C \in \mathbb{R}^{m \times k}$ 로 표현되며, 요소 $c_{ij}$ 는 다음과 같이 계산된다.
\[c_{ij} = \sum_{l=1}^{n} a_{il}b_{lj} ,\qquad i = 1,\dots,m,\quad j = 1,\dots,k.\]식을 보면, $c_{ij}$ 를 구하기 위해 행렬 $A$ 의 $i$ 번째 행과, 행렬 $B$ 의 $j$ 번째 열을 곱해야 하며,
행렬곱은 요소별 계산(element-wise operation)으로 이루어지지 않는다는 점을 알 수 있다.
또한, 행렬곱을 위해서는 행렬 $A$ 와 $B$ 는 인접한 차원(dimension)이 아래와 같이 같아야한다.
\[\underbrace{A}_{n \times k}\underbrace{B}_{k \times m}=\underbrace{C}_{n \times m}\]아다마르 곱(Hadamard product)
같은 크기의 두 행렬의 각 성분을 곱하는 연산으로 아다마르 곱이 존재한다.
즉, 요소별 계산(element-wise operation)을 하며 아다마르곱은 덧셈에 대하여 분배 법칙을 따르고 다음과 같이 표현된다.
$$
M \bigcirc N =
\begin{bmatrix}
M_{11}N_{11}&M_{12}N_{12}&\dotsm &M_{1n}N_{1n}\\
M_{21}N_{21}&M_{22}N_{22}&&M_{2n}N_{2n}\\
\vdots &&\ddots &\vdots \\
M_{m1}N_{m1}&M_{m2}N_{m2}&\dotsm &M_{mn}N_{mn}
\end{bmatrix}
\in \operatorname {Mat} (m,n;R)
$$
단위 행렬(Identity Matrix)
행렬을 계산할 때 특별히 자주 사용되는 행렬들 중 가장 중요한 행렬인 단위 행렬에 대해서 알아보자.
단위 행렬(또는 항등 행렬)은 모든 대각성분 요소가 1, 나머지 요소는 0인 행렬으로, $\mathbb{R}^{n \times n}$ 에서 아래와 같이 표현된다.
\[I_{n} := \begin{bmatrix} 1 & 0 & \cdots & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 & \cdots & 1 \\ \end{bmatrix} \in \mathbb{R}^{n \times n}\]행렬의 성질
이제 위에서 정의한 행렬합, 행렬곱, 단위 행렬을 이용하여 행렬곱의 성질에 대해 알아보자.
-
결합법칙 :
\[\forall A \in \mathbb{R}^{m×n}, B \in \mathbb{R}^{n×p}, C \in \mathbb{R}^{p×q} : (AB)C = A(BC)\] -
분배법칙 :
\[\forall A, B \in \mathbb{R}^{m×n}, C, D \in \mathbb{R}^{n×p} : \begin{matrix} (A+B)C = AC + BC \\A(C+D) = AC+AD \end{matrix}\] -
단위 행렬과의 곱 :
\[\forall A \in \mathbb{R}^{m×n} : I_{m}A = AI_{n} = A\] \[(\;단, \; m \neq n \; 일 \; 때 ,\; I_{m} \neq I_{n}\;)\] -
\[AB \neq BA\]교환법칙:행렬곱은 교환법칙이 성립하지 않는다.
아래 예시 2.3 와 함께 알아보자.
예시 2.3
\[A = \begin{bmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{bmatrix} \in \mathbb{R}^{2 \times 3}, \quad B = \begin{bmatrix} 0 & 2 \\ 1 & -1 \\ 0 & 1 \end{bmatrix} \in \mathbb{R}^{3 \times 2} \; 일 \; 때,\] \[\begin{align} & AB = \begin{bmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{bmatrix} \begin{bmatrix} 0 & 2 \\ 1 & -1 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 2 & 3 \\ 2 & 5 \end{bmatrix} \in \mathbb{R}^{2 \times 2}, \\ & BA = \begin{bmatrix} 0 & 2 \\ 1 & -1 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{bmatrix} = \begin{bmatrix} 6 & 4 & 2 \\ -2 & 0 & 2 \\ 3 & 2 & 1 \end{bmatrix} \in \mathbb{R}^{3 \times 3}. \end{align}\] \[\therefore \; AB \neq \ BA\]
역행렬과 전치행렬
역행렬(Inverse)
정사각행렬 $A$ 와 $B$ 가 $AB = I_{n} = BA$ 를 만족할 때 $(\;단, \; A \in \mathbb{R}^{n \times n}, \; B \in \mathbb{R}^{n \times n}\;)$
$B$ 를 $A$ 의 역행렬(Inverse) 이라 하고, $A^{-1}$ 라고 표현한다.
다만, 모든 행렬 $A$ 가 역행렬 $A^{-1}$ 를 가지는 것은 아니다.
역행렬은 하나의 행렬에 대해서 유일하며, 바로 다음 Chapter 3 에서 역행렬을 구하는 방법에 대해서 알아볼 것이다.
역행렬이 존재하는 행렬은 정칙 행렬(regular) / 가역 행렬(invertible) / 비특이 행렬(non-singular)이라고 불리우고,
역행렬이 존재하지 않는 행렬은 특이 행렬(singular) / 비가역 행렬(non-invertible) 이라고 불린다는 점도 알아두자.
예시 2.4
\[A = \begin{bmatrix} 1 & 2 & 1 \\ 4 & 4 & 5 \\ 6 & 7 & 7 \end{bmatrix} , \quad B = \begin{bmatrix} -7 & 7 & 6 \\ 2 & 1 & -1 \\ 4 & 5 & -4 \end{bmatrix} \; 일 \; 때,\]
$AB = I = BA$ 이고, A와 B는 서로 역행렬 관계이다.
전치행렬(Transpose)
행렬 $A$, $B$ 의 각각의 요소가 $a_{ij} = b{ji}$ 일 때, $B$ 를 $A$ 의 전치행렬이라고 하며, $B = A^{T}$ 라고 한다. $( \; A \in \mathbb{R}^{m \times n}, \; B \in \mathbb{R}^{n \times m} \; )$
일반적으로, $A$ 의 열을 $A^{T}$ 의 행에 나열해서 $A^{T}$ 를 얻을 수 있다.
역행렬과 전치행렬의 중요한 성질들은 아래와 같다.
\[\begin{align} AA^{-1} &= I = A^{-1}A \\ (AB)^{-1} &= B^{-1} A^{-1} \\ (A+B)^{-1} &\neq A^{-1} + B^{-1} \\ (A^{T})^{T} &= A \\ (A+B)^{T} &= A^{T} + B^{T} \\ (AB)^{T} &= B^{T}A^{T} \end{align}\]대칭행렬(Symmetric Matrix)
대칭행렬은 정사각행렬에서 대각선에 대칭인 두 원소가 같은 행렬을 말한다.
즉, 정사각행렬의 원소 $a_{ij}$ 와 원소 $a_{ji}$ 가 같은 행렬이다 : $A = A^{T} ( \; 단, \; A \in \mathbb{R}^{n \times n} \; )$
임의의 두 대칭행렬의 합은 항상 대칭행렬이라는 특징이 있다.
스칼라 곱셈
행렬에 스칼라 $\lambda$ 가 곱해질 때의 특징을 알아보도록 하자.
행렬 $A \in \mathbb{R}^{m \times n}$ 와 스칼라 $\lambda \in \mathbb{R}$ 에 대해서 $\lambda A = K \; 일 \; 때,$ $K_{ij} = \lambda a_{ij}$ 이다.
즉, 행렬 $A$ 의 모든 요소에 스칼라값 $\lambda$ 가 곱해지는 연산이다.
다음 수식들을 통해 행렬에 대한 스칼라 $\lambda, \psi $ 의 곱셈의 특징들을 확인할 수 있다.
- 결합법칙 :
- $(\lambda \psi)C = \lambda (\psi C), \quad C \in \mathbb{R}^{m \times n}$
- $\lambda (BC) = (\lambda B)C = B(\lambda C) = (BC)\lambda , \quad B \in \mathbb{R}^{m \times n}, \; C \in \mathbb{R}^{n \times k} .$
- 분배법칙 :
- $(\lambda C)^{T} = C^{T}\lambda^{T} = C^{T}\lambda = \lambda C^{T} \quad (\; \because \; \lambda = \lambda^{T} \; )$
- $(\lambda + \psi)C = \lambda C + \psi C,\quad C \in \mathbb{R}^{m \times n}$
$\lambda (B + C) = \lambda B + \lambda C,\quad B,C \in \mathbb{R}^{m \times n}$
연립 일차 방정식의 간단한 표현
다음과 같은 연립 일차 방정식이 있다고 해보자.
\[\begin{matrix} 2x_{1}\\4x_{1}\\9x_{1} \end{matrix} \begin{matrix} +\\-\\+\\ \end{matrix} \begin{matrix} 3x_{2}\\2x_{2}\\5x_{2}\\ \end{matrix} \begin{matrix} +\\-\\- \end{matrix} \begin{matrix} 5x_{3}\\7x_{3}\\3x_{3} \end{matrix} \begin{matrix} =\\=\\= \end{matrix} \begin{matrix} 1\\8\\2 \end{matrix}\]행렬 곱셈의 정의에 의하여,
연립 일차 방정식의 계수행렬(coefficient matrix) $A$ 와 함께 $Ax = b$ 의 형태로 표현 가능하다.