매개 변수 추정
Chapter 2 : Parameter Estimation
-
목차
선형회귀 setting이 된 상태에서 다음과 같은 데이터셋이 있다고 가정을 해보자
\[D := [(x_1,y_1),...,(x_n,y_n)]\] \[input \ x_n \subseteq \mathbb{R}^D , traget \ y_n \subseteq \mathbb{R}, n = 1,..,N\]이때 input 값인 $ x_i, x_j $ 는 해당 target 값인 $ y_i, y_j $에 대해 조건부 독립이기 때문에 Likelihood factorize하여 다음과 같이 표현할 수 있다.
\[\prod_{n=1}^N p(y_n | x_n, \theta ) = \prod_{n=1}^N \mathcal{N}(y_n | x^T_n \theta , \sigma^2 )\]여기서 우리는 최적의 파라미터 $ \theta^* \subseteq \mathbb{R}^D $ 를 구하고 이것을 input값인 $ x $ 와 같이 넣어 target 값인 $ y $ 의 분포를 구하려고 한다. 해당 수식은 다음과 같다.
\[p(y_* | x_*, \theta^*) = \mathcal{N} ( y_*| x^T_* \theta^* , \sigma^2 )\]이번 장에서는 위의 수식으로 구해지는 Likelihood를 최대화시켜 파라미터를 추정하려고 한다.
최대우도법 (Maximum Likelihood Estimation)
Likelihood를 최대화한 파라미터 $ \theta _{ML}$ 을 찾는 과정인 Maximum Likelihood estimation를 우리는 가장 넓게 쓰고 있다. 이것은 trainin data의 predictive 분포를 최대화시킨다는 것으로 다음과 같이 구해진다.
\[\theta_{ML} = arg \underset{ \theta } {max} \ p( \mathcal{Y} | \mathcal{X}, \theta)\]이때 주의해야할 점은 Likelihood $ p(y | x, \theta) $ 는 $ \theta $ 의 확률 분포가 아니기 때문에 이것을 합해도 1이 되지 않는다. 또한 각 \theta에 대해 합을 구하는 것도 불가능하며 위의 식은 y에 대한 normalized probabilty 분포이다.
우리는 해당 likelihood를 최대한 시키는 $ \theta_{ML} $ 을 구하기 위해 gradient ascent, descent을 사용하게 된다. 또한 우리는 바로 likelihood를 최대화하지 않고 log 변형을 적용시키게 된다.
로그 변환 (Log Transformation)
likelihood는 N개의 가우시안 분포이다. 이때 log-transformation을 적용시키면 미분이 간편해지고, 언더플로우가 발생하지 않게 된다. 로그 변환을 적용시킨 $ \theta_{ML} $ 을 찾는 수식은 다음과 같다.
\[-log( \mathcal{Y} | \mathcal{X} , \theta ) = -log \prod_{n=1}^N p(y_n | x_n, \theta ) = - \sum_{n=1}^N log p(y_n|x_n, \theta )\]선형회귀 모델에서 likelihood는 로그변환을 하면 아래와 같이 표현할 수 있습니다. (선형회귀모델에서 likelihood는 가우시안 분포를 따름)
\[logp(y_n | x_n, \theta ) = - \frac{1}{2 \sigma^2 } ( y_n - x^T_n \theta)^2 + const\]이때 negative log-likelihood를 취하면 아래와 같은 식을 얻을 수 있다. 이때 const값은 $ \theta $ 와 독립이기 때문에 무시하고 계산할 수 있다.
\[\mathcal{L}( \theta ) := \frac {1}{2 \sigma^2 } \sum{n=1}^N (y_n - x^T_n \theta) ^2 \\ = \frac{1}{2 \sigma^2} (y-X \theta )^T (y- X \theta ) = \frac{1}{2 \sigma^2} \lVert y-X \theta \rVert ^2\]우리는 이것을 미분하여 다음과 같이 Gradient를 계산할 수 있다.
\[\frac{d \mathcal{L} }{d \theta} = \frac{d}{d \theta} ( \frac{2 \sigma^2}{1} (y - X \theta )^T (y- X \theta ))\\ = \frac{1}{2 \sigma^2} \frac{d}{d \theta } (y^T y - 2y^T X \theta + \theta^T X^T X \theta ) = \frac{1}{\sigma^2}(- y^T X + \theta^T X^T X) \subseteq \mathbb(R)^{1 \times D}\]우리는 또한 $ \frac{d mathcal{L}}{d \theta} = 0^T $ 로 다음과 같은 수식을 유도할 수 있다.
\[\frac{d mathcal{L}}{d \theta} = 0^T \iff \theta^T_{ML} X^T X = y^T X \\ \iff \theta^T_{ML} = y^T X ( X^T X ) ^{-1}\\ \iff \theta_{ML} = (X^T X)^{-1} X^T y\]linear regression 모델은 현실적인 데이터에서 충분한 설명을 이끌어내지 못한다. 그래서 우리는 좀 더 non-linear한 모델을 다루게 될 것이다. non-linear한 모양을 하는 회귀모델도 Parameter가 linear하다면 우리는 이를 linear regression이라고 할 수 있으며 우리는 이런 경우 non-linear transformation을 다음과 같이 나타낼 수 있다.
\[p(y|x, \theta ) = \mathcal{N} (y| \phi^T (x) \theta, \sigma^2 ) \iff y = \phi^T (x) \theta + \epsilon = \sum_{k=0}^{K-1} \theta_k \phi_k (x) + \epsilon\]다항 회귀(Polynomial Regression)
우리는 regression에서 $ y = \phi^T (x) \theta + \epsilon $ 을 구하는 과정에서 $ \phi (x) $ 를 다음과 같이 나타낼 수 있다.
\[\phi(x) = \begin{bmatrix} \phi_0 (x) \\ \phi_1 (x) \\ \vdots \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ x \\ x^2 \\ x^3 \\ \vdots \\ x^{K-1} \end{bmatrix} \subseteq \mathbb{R}^K\]또한 $ \phi_j (x_i) $ 의 transpose는 다음과 같이 나타낼 수 있다.
\[\Phi := \begin{bmatrix} \phi^T (x_N) \\_ \vdots \\ \phi^T (x_N) \end{bmatrix} = \begin{bmatrix} \phi_0 (x_1) & \cdots & \phi_{K-1}(x_1) \\ \phi_0 (x_2) & \cdots & \phi_{K-1}(x_2) \\ \vdots & \vdots \\ \phi_0 (x_N) & \cdots & \phi_{K-1}(x_N) \\ \end{bmatrix} \subseteq \mathbb{R}^{N \times K}\]다항회귀의 최대 우도 적합 (Maximum Likelihood Polynomial Fit)
그림1 다항 회귀의 최대 우도
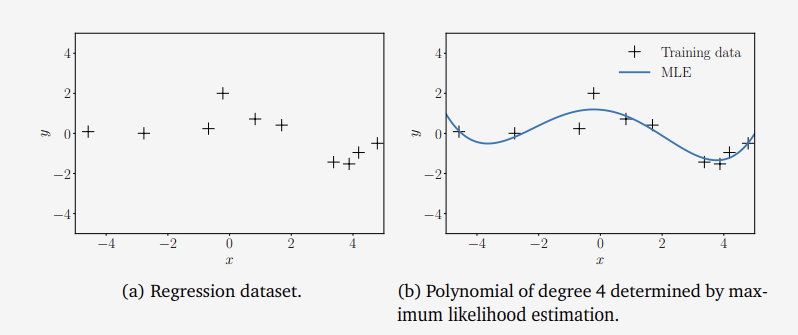
위의 그림(a)는 N = 20의 $ (x_n, y_n) $로 이루어진 데이터셋이다. 이 때 $ x_n \sim \mathcal{U} [-5,5]$ 이고 $ y_n = -sin(x_n / 5) + cos(x_n) + \epsilon, \epsilon \sim \mathcal{N} (0,0.2^2) $ 이다.
우리는 이런 데이터셋을 4차 변환으로 maximum likelihood estimation하여 그림 (b)과 같이 $ \theta_{ML} $ 을 구해 Regression 함수를 구할 수 있다.
Estimation the Noise Variance
우리는 지금까지 $ \theta^2 $가 주어진 상태에서 계산을 진행하였고 이장에서는 Maximum likelihood estimation의 원칙을 이용하여 $ \theta_{ML}^2 $ 을 직접 계산하려고 한다. 해당 과정은 다음과 같다.
\[log p( \mathcal{Y} | \mathcal{X}, \theta , \sigma ^2 ) = \sum_{n=1}^N log \mathcal{N} (y_n | \phi^T (x_n) \theta , \sigma^2) \\ = \sum_{n=1}^N ( - \frac{1}{2} log (2 \pi ) - \frac{1}{2} log \sigma^2 -\frac{1}{2 \sigma^2}(y_n - \phi^T (x_n) \theta )^2 ) \\ = - \frac{N}{2} log \sigma^2 - \frac{1}{2 \sigma^2} \sum_{n=1}^N (y_n - \theta^T(x_n)\theta)^2 + const\]이후에 $ \sigma^2 $ 에 대해 미분을 하면 다음과 같이 최종적은 결과를 얻을 수 있다.
\[\frac{\partial log p( \mathcal{Y} | \mathcal{X}, \theta , \sigma^2 )}{ \partial \sigma^2 } = \frac{N}{2 \sigma^2 } + \frac{1}{2 \sigma^4 } s = 0\\ \iff \frac{N}{2 \sigma^2 } = \frac{s}{2 \sigma^4} \\ \\ \sigma^2_{ML} = \frac{s}{N} = \frac{1}{N} \sum_{n=1}^N (y_n - \phi^T(x_n) \theta )^2\]선형 회귀 과적합(Overfitting in Linear Regression)
우리는 방금까지 maximum likelihood estimation를 사용하여 linear 모델을 학습을 시키는 것에 대해 이야기하였다. 우리는 오차와 손실을 계산하여 모델을 평가할 수 있는데 maximum likelihood estimation에서는 negative log-likelihood를 최소화는 방법을 쓸 수 있다. 또한 노이즈 파라미터 $ \sigma^2 $ 가 free model parameter가 아니면 $ \frac{1}{ \sigma^2 } $ 로 스케일링 하지 않아도 되고 이런 경우 우리는 제곱오차(squared-error-loss)가 아닌 root-mean-square-error(RMSE)를 주로 사용하게 된다.
\[\sqrt( \frac{1}{N} \lVert y-\Phi \theta \rVert^2) = \sqrt( \frac{1}{N} \sum_{n=1}^N (y_n - \phi^T (x_n) \theta )^2),\]제곱 오차의 경우 크기가 다른 데이터셋의 오차를 비교할 수 있고, RMSE의 경우 관측된 함수 값 $ y_n $과 동일한 스케일 및 단위를 가질 수 있다.
트레이닝 데이터 개수 N, 다항식의 차 수 M이라고 가정을 하자 우리는 이때 $ 0 \leq M \leq N -1 $ 을 M의 개수로 하는 것이 적절하다. 반대로 $ M \ge N $ 의 경우 데이터 포인트보다 더 많은 파라미터를 가지게 되고 이 때 가능한 MLE는 무수히 많게 된다.
그림2 다양한 다항회귀에서의 최대우도적합
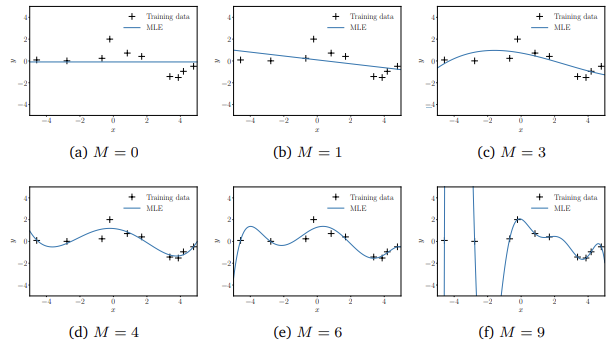
위의 그림은 10개의 데이터 포인터에 대해 다항식의 차수를 보여준다. 차수가 높아질 수록 점차 데이터에 적합해지는 것을 알 수 있고, M=9일 때 모든 데이터와 일치한다. 하지만 이런 경우에는 새로운 데이터에 대해서 예측을 못하는 경우가 있으며 이를 overfitting되었다고 한다.
우리는 그렇기에 새로운 데이터를 잘 설명하기 위해 일반화하는 것이 필요하다. 200개의 테스트 셋을 별도로 구성하여 다항식 차수 M에 대한 일반화 성능에 대해 알아보고자 한다. 테스트의 input으로는 [-5,5] 안의 값의 200 포인트의 선형 그리드를 선택을하며 결과는 다음과 같다.
그림3 훈련 및 테스트 에러
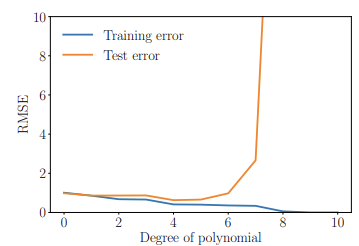
test결과 차수가 6차부터 성능이 급격하게 주는 것을 알 수 있었다. 4차에서 가장 작은 테스트 오차를 보였으며 우리는 이 지점에서 일반화가 가장 잘 됐다는 것도 알 수 있다.
최대 사후 확률 (Maximum A Posteriori Estimation)
파라미터 $ \theta $ 에 대한 가우시안 사전확률에서 선형 회귀에서 음의 로그 사후 확률은 아래와 같다.
\[-logp( \theta | \mathcal{X}, \mathcal{Y} ) = \frac{1}{2 \sigma^2 } (y- \Phi \theta )^T (y - \Phi \theta) + \frac{1}{2b^2} \theta^T \theta + const\]위의 식을 파라미터 $ \theta $ 에 대해 미분을 하여 로그 사후 확률의 경사를 아래와 같이 구할 수 있다.
\[- \frac{d log p( \theta | \mathcal{X} , \mathcal{Y} )}{d \theta } = \frac{1}{ \sigma^2 } ( \theta^T \Phi^T \Phi - y^T \Phi ) + \frac{1}{b^2} \theta^T\]우리는 MAP 추정치 $ \theta_{MAP} $ 을 위의 경사를 0^T로 설정하여 다음과 같이 풀 수 있다.
\[\frac{1}{ \sigma^2 } ( \theta^T \Phi^T \Phi - y^T \Phi) + \frac{1}{b^2} \theta^T = 0^T \\ \iff \theta^T ( \frac{1}{\sigma^2} \Phi^T \Phi + \frac{1}{b^2} I ) - \frac{1}{ \sigma ^2} y^T \Phi = 0^T \\ \iff \theta^T ( \Phi^T \Phi + \frac{\sigma^2}{b^2} I ) = y^T \Phi \\ \iff \theta^T = y^T \Phi ( \Phi^T \Phi + \frac{ \sigma^2 }{b^2} I )^{-1}\]이제 $ \theta_{MAP} $ 은 양변을 transpose하여 아래와 같이 나타낼 수 있다.
\[\theta_{MAP} = (\Phi^T \Phi + \frac{ \sigma^2 }{ b^2 } I )^{-1} \Phi^T y\]
$ \theta_{ML} $ 과 MLE를 비교해보면 역행렬 안에 $ \frac{\sigma^2}{b^2} $ 가 추가되어 있는 것을 알 수 있다. 이 항은 대칭적이며 positive definite하다는 것을 보장한다. 즉 역이 존재하고 $ \theta_{ML} $ 가 선형방적식 시스템의 유일한 해임을 보장하며 정규화를 반영한다.
다항 회귀에 대한 최대 사후 확률 (MAP Estimation for Polynomial Regression)
우리는 앞서 다항식 회귀 분석 예에서 파라미터 $ \theta $ 에 대한 가우시안 사전확률 $ p( \theta ) = \mathcal{N} (0,1) $ 을 설정하고 이에 $ \theta_{ML} $ 을 결정한다. 아래 그림은 6차와 8차 다항식에 대한 최대 우도와 MAP 추정치를 보여준다.
그림4 다항회귀 : 최대우도와 최대사후추정(MAP)
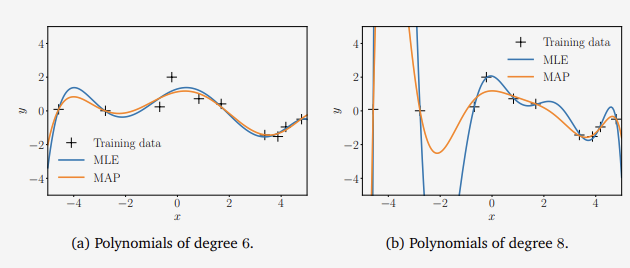
여기서 우리는 사전확률이 낮은 차수의 다항식에서는 큰 역할을 하지 않지만 높은 차수의 다항식에서는 비교적으로 많은 영향을 주는 것을 알 수 있다. MAP 추정치가 과적합의 경계와 가까워질 수 있지만, 이 문제는 일반적인 해결책이 아니기 때문에 좀 더 원칙적인 접근이 필요하다.
정규화로써 최대 사후 확률(MAP Estimation as Regularization)
매개변수 $ \theta $ 에 사전 확률 분포로 설정하는 대신 정규화를 통해 매개변수 진폭에 페널티를 부과하여 과적합의 영향을 완화할 수 있다. 정규화된 최소 제곱에서, $ \theta $에 대해 최소화해야하는 손실 함수는 아래와 같다.
\[- \log p( \theta ) = \frac{1}{2b^2} \lVert \theta \rVert _{2}^{2}\]이때, 첫번째 항은 데이터의 적합성을 나타내주는 항이며, 두번째 항은 정규화 항으로 정규화 매개변수 $ \lambda \geq 0 $ 는 정규화의 수준을 조절한다.
Regularizer $ \lambda \lVert \theta \rVert _{2}^{2} $ 는 음의 로그 가우시안 사전 확률 분포로 해석 될 수 있으며 MAP의 추정에 사용된다. 이때 가우시안 사전확률 분포 $ p( \theta ) = \mathcal{N} (0, b^2 I) $ 을 사용하여 아래와 같은 음의 로그 가우시안 사전 확률을 얻을 수 있다.
\[- \log p ( \theta ) = \frac{1}{2 b^2 } \lVert \theta \rVert _{2}^{2} + const\]이 때 $ \lambda = \frac{1}{2b^2} $ 일 때 정규화 항과 음의 로그 가우시안 사전 확률은 같게 된다.
정규화된 최소 제곱 손실 함수를 최소화하면 아래와 같은 식을 얻을 수 있다.
\[\theta_{RLS} = ( \Phi^T \Phi + \lambda I)^{-1} \Phi^T y\]이는 $ \lambda = \frac{ \sigma^2 }{ b^2 } $ 에 대한 MAP 추정치와 같고, 여기서 $ \sigma^2 $ 는 noise에 대한 분산이고 $ b^2 $은 가우시안 사전 확률의 분산이다.