PCA의 저차원 근사
Chapter 4 : PCA with Low-Rank Approximation
PCA with Low-Rank Approximation
앞서 논의했던 대로 $X = [x_1, \cdots, x_N]$ 에 대한 공분산 행렬 $\boldsymbol{S}$ 는 다음과 같다.
\[\boldsymbol{S} = {1 \over N} \sum_{n=1}^N x_n x_n^\textsf{T} = {1 \over N} \boldsymbol{X} \boldsymbol{X}^\textsf{T}, \tag{10.32}\] \[\boldsymbol{X} = [x_1,\ldots, x_N] \in \mathbb{R}^{D \times N}. \tag{10.32}\]이러한 $\boldsymbol{S}$에 대한 eigenvalue를 구하는 방법은 다음과 같이 2가지로 나뉜다.
- $X X^\textsf{T}$를 계산하여 $\boldsymbol{S}$의 eigendecomposition을 통해 eigenvalues와 eigenvectors를 직접 계산한다.
- $\boldsymbol{S}$가 대칭행렬이고 $X X^\textsf{T}$로 분해가능하므로 $\boldsymbol{S}$의 eigenvalue $\lambda_d$는 $X$의 singluar value $\sigma_d$에 대해 $\lambda_d = {\sigma_d ^2 \over N}$을 통해 구할 수 있다.
2번에 대해 조금 더 자세히 설명하자면, $X$는 singular value decomposition에 의해 $X = U \Sigma V^\textsf{T}$로 표현가능하므로 아래와 같은 식을 구할 수 있어 $\boldsymbol{S}$의 singular matrix $\Sigma_S = {1\over N} \Sigma \Sigma^\textsf{T}$이다.
\[\boldsymbol{S} = {1 \over N} \boldsymbol{X} \boldsymbol{X}^\textsf{T} = {1 \over N} \boldsymbol{U} \boldsymbol{\Sigma}\underbrace{\boldsymbol{V}^\textsf{T}\boldsymbol{V}}_{=\boldsymbol{I}_N} \boldsymbol{\Sigma}^\textsf{T}\boldsymbol{U}^\textsf{T} = {1 \over N} \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{\Sigma}^\textsf{T} \boldsymbol{U}^\textsf{T}. \tag{10.32}\]즉, $S$의 가장 큰 $M$개의 eigenvalue는 곧 $X$의 가장 큰 $M$개의 eignevalue와 연관되므로, 다음과 같이 truncated SVD를 통해 $\tilde{X}_M$을 구할 수 있다.
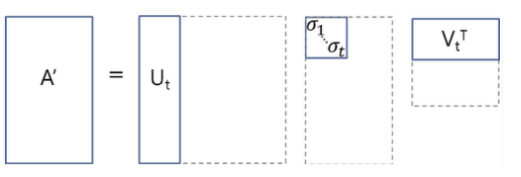
\[\underbrace{\boldsymbol{X}}_{D \times N} = \underbrace{\boldsymbol{U}}_{D \times D} \underbrace{\boldsymbol{\Sigma}}_{D \times N} \underbrace{\boldsymbol{V^\textsf{T}}}_{N \times N} ,\tag{10.32}\] \[\tilde{\boldsymbol{X}}_M = \underbrace{\boldsymbol{U_M}}_{D \times M} \underbrace{\boldsymbol{\Sigma_M}}_{M \times M} \underbrace{\boldsymbol{V^\textsf{T}_M}}_{M \times N} \in \mathbb{R}^{D \times N} \tag{10.32}\][그림 6] PCA with Truncated SVD
출처
실제로 지금까지 설명한 방법을 적용하기 위해서는 eigenvalues 또는 singular values를 구해야 하는데, 행렬의 크기가 커지면 특성 방정식의 근을 쉽게 찾기가 어려워진다.
그러므로 현재 선형대수와 관련된 package에서 제공하는 eigenvalue 및 singular value를 구하는 방법들은 iterative한 방법을 사용한다.
또한, PCA를 적용하는 대부분의 경우 eigenvectors가 전부 필요한 게 아니라 몇 개의 eigenvectors만 필요하기 때문에, 각 iteration마다 가장 큰 eigenvalue에 해당하는 eigenvector만을 구하면 된다.
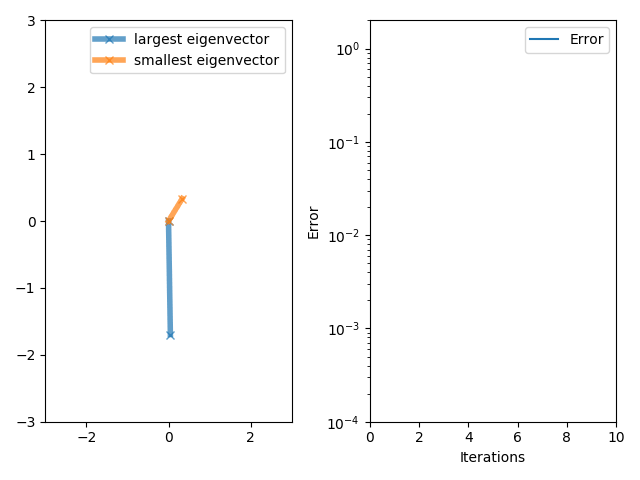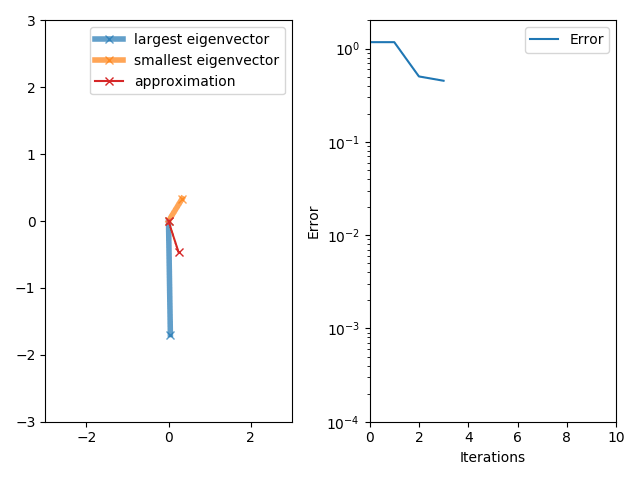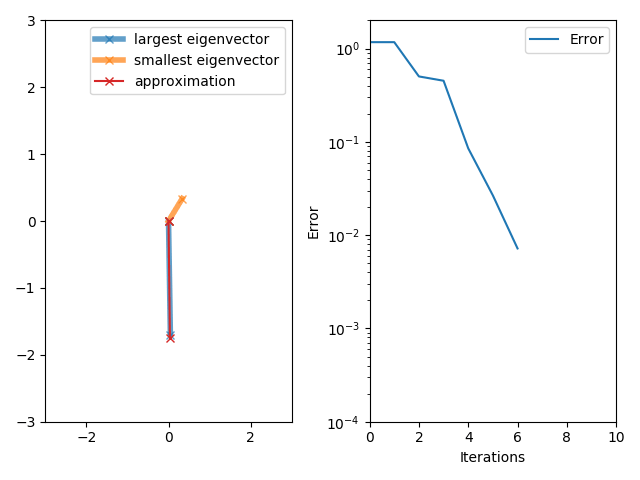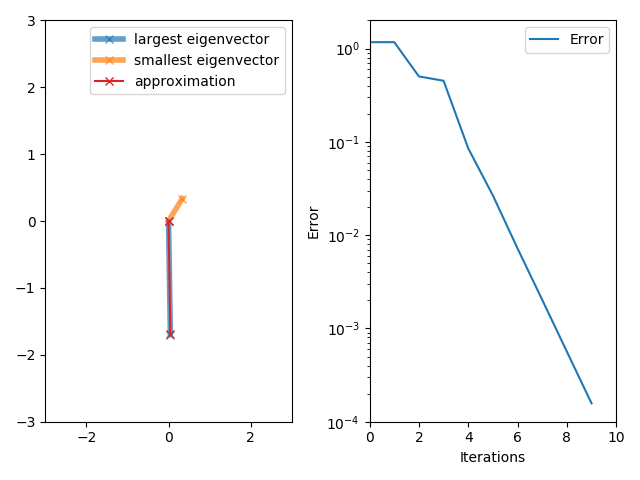
이러한 eigenvector는 수식 (10.32)로 표현되는 power iteration에 의해서 구할 수 있다.
\[x_{k+1} = {\boldsymbol{S} x_k \over \lVert \boldsymbol{S} x_k \rVert}, \quad k=0,1,\ldots . \tag{10.32}\][그림 7] Example of power iteration