정사영
Chapter 8 : Orthogonal Projection
-
목차
Orthogonal Projection
machine learning에서는 high-dimensional data를 주로 다루는데 이런 데이터를 그대로 압축하거나 시각화하는 경우 정보 손실이 일어난다 따라서 압축 손실을 줄이기 위해 데이터에서 중요한 dimension을 찾아야 한다
3.8.1 Projection onto one-dimensional subspaces
3.8.2 projection onto general subspaces
개념을 확장하여 x를 더 낮은 차원의 U로 projection하는 경우를 살펴보면 one-dimension 이상의 general space로 개념이 확장된다
3.8.3 Gram-schmidt orthogonalization
다음은 내적 공간에서 유한개의 일차독립 벡터 집합을 정규 직교 기저로 변환하는 내용을 다룬다. 쉽게 말하자면 두 벡터가 있을 때 한 벡터와, 그 벡터가 가지고 있는 성분을 빼줌으로써 두 벡터가 서로 직교하게 만드는 것이다.
3.8.4 projection onto affine subspaces
지금까지는 vector를 어떻게 더 낮은 차원의 subspace U로 projection할지에 대한 방법에 대해 얘기했는데 이번 장에서는 vector를 affine subspace로 projection하는 방법에 대해 다룬다.
affine space란 유클리드 공간의 affine 기하학적 성질들을 일반화해서 만들어지는 구조로, affine space에서는 점과 점을 빼서 벡터를 얻거나 점에 벡터를 더해 다른 점을 얻을 수는 있지만 원점이 없으므로 점과 점을 더할 수는 없다.
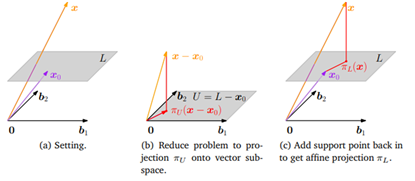
그림1 affine subspace
아래 그림을 봤을 때 affine space $L$과 $U$의 basis가 주어져있다 $x$의 $L$위로의 orthogonal projection을 구하기 앞서 우리가 아는 형태로 변형시키면 쉽게 풀 수 있다. 따라서 그림 (b)와 같이 $x$와 $L$에 공통적으로 $x_0$를 빼줘서 $x-x_0$를 $b_1, b_2$가 basis인 subspace $U$로 projection하는 문제로 바꿔서 풀 것이다. 즉 공간은 $L$에서 $L-x_0$로 변형, $x$는 $x-x_0$로 변형, $x_0$는 $x-x_0$의 projection으로 변형한 것이다. 이를 식으로 표현하면 다음과 같다
그림2 식
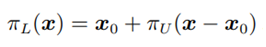
또한 그림 (c)를 보면 $x$와 $L$사이의 거리가 $x-x_0$와 $U$사이의 거리와 같다는 것을 알 수 있다 이를 식으로 표현하면 다음과 같다
그림3 식
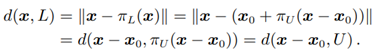
그림4 projection onto affine subspaces