선형 매핑
Chapter 7 : Linear Mappings
-
목차
이전 챕터 Chapter 2-6 에서 선형방정식 $Ax=b$에서 행렬 $A$의 특징을 살펴보았다.
그러한 $A$의 특성이 선형 방정식을 푸는데 왜 중요한 것일까?
이번 챕터에서는 행렬 $A$가 갖는 의미에 대해서 살펴보도록 하겠다.
Definition of Linear Mappings
행렬 $A \in \mathbb{R}^{m \times n}$에 대해 $Ax$의 연산을 생각해보면 행렬 $A$는 $n$차원 벡터 $x$를 $m$차원 벡터로 변환해주는 연산자라는 것을 알 수 있다.
행렬 $A$는 덧셈에 대해 닫혀있고, Chapter 2-2 에서 살펴보았듯이 스칼라 곱셈에 대해 닫혀있다.
이러한 선형성이 유지되는 사상(또는 변환)을 선형 사상(Linear Mappings) 이라 한다.
즉, 벡터 공간 $V$에서 벡터 공간 $W$로 변환해주는 사상 $\Phi : V \rightarrow W$는 다음 조건을 만족하는 사상이며, 이러한 선형 사상은 벡터 공간을 보존하면서 변환시켜준다는 특징이 있다. 1
임의의 벡터 $x, y \in V$와 $\lambda \in \mathbb{R}$에 대해
\[\Phi(\bf{x} + \bf{y}) = \Phi(\bf{x}) + \Phi(\bf{y})\] \[\Phi(\lambda \bf{x}) = \lambda \Phi(\bf{x})\]
Injective, Surjective, Bijective
이러한 선형 사상의 특징을 규정하기 위해 다음과 같은 특별한 조건을 만족하는 선형 사상들을 정의한다.
- 단사(Injective) : 일대일 대응을 만족한다.
\[\forall x, y \in V, \forall \lambda, \psi \in \mathbb{R} : \Phi(\lambda x + \psi y) = \lambda \Phi (x) + \psi \Phi (y)\]
- 전사(Surjective) : 치역과 공역이 같다.
\[\Phi (V) = W\]
- 전단사(Bijective) : 전사와 단사를 모두 만족한다.
Isomorphism
선형 방정식 $Ax = b$이 임의의 $b$에 대해 유일한 해를 가지려면 사상 $\Phi : x \rightarrow Ax$가 전단사 사상이어야 하며, 전단사 사상은 역사상(inverse mapping) $\Phi^{-1}$가 존재한다.
즉, $A^{-1}$가 존재하기 위해서는 $\Phi : x \rightarrow Ax$가 전단사 사상이어야 한다. 따라서 우리는 아래와 같이 사상을 분류하기로 한다.
- Isomorphism : 사상 $\Phi : V \rightarrow W$ 가 전단사 선형(bijective linear)이다.
\[\exists A^{-1} ~ for ~ A \in \mathbb{R}^{m \times n}\]
- Endomorphism : 사상 $\Phi : V \rightarrow V$ 가 선형(linear)이며 정의역과 공역이 같다.
\[A \in \mathbb{R}^{n \times n}\]
- Automorphism : 사상 $\Phi : V \rightarrow V$ 가 전단사 선형(bijective linear)이며, 정의역과 공역이 같다.
\[\exists A^{-1} ~ for ~ A \in \mathbb{R}^{n \times n}\]
- Identity Automorphism, id$_{V}$ : 사상 $\Phi : V \rightarrow V$에 대해 $\Phi(x) = x$
\[A = I \in \mathbb{R}^{n \times n}\]
여기서 굉장히 중요한 정리가 등장한다.
유한 벡터 공간 $V$와 $W$이 isomorphic한 것은 $dim(V)=dim(W)$과 필요충분 조건이다.
두 벡터 공간이 isomorphic 하다는 것은 isomorphic한 사상 $\Phi : V \rightarrow W$ 또는 $\Phi : W \rightarrow V$가 존재한다는 뜻이다.
즉, 벡터 공간 $V$에서 $W$로 변환하는 과정에서 $V$의 전체 차원수와 $W$의 전체 차원수만 같다면 어떠한 정보 손실도 없이 변환이 가능하다는 것이다.
따라서 $X \in \mathbb{R}^{m \times n}$인 행렬 X를 $x \in \mathbb{R}^{mn \times 1}$인 벡터로 표현가능하다는 뜻이며, 이것은 우리가 Machine learning에서 (64,64,3)인 입력 이미지를 (64x64x3, 1)의 단일 column vector로 변환해서 입력할 수 있게 해준다.
추가로 선형사상과 isomorphism 각각 아래와 같은 성질을 만족한다.
- 선형 사상 $\Phi : V \rightarrow W$와 $\Psi : W \rightarrow X$에 대해 사상 $\Psi \circ \Phi : V \rightarrow X$ 또한 선형사상이다.
- 사상 $\Phi : V \rightarrow W$가 isomorphism이면 $\Phi^{-1} : W \rightarrow V$ 또한 isomorphism이다.
Matrix Representation of Linear Mapping
n 차원의 서로 Isomorphic한 Vector Space가 있을 때 Vector Space의 basis는 순서가 중요
Vector Space V의 순서 기저(ordered basis) 는 기저에 순서를 준 것을 의미
-> 즉, V의 기저를 집합이 아니라 튜플(순서쌍)으로 본 것
V 라는 Vector Space의 bases를 {b1, b2, b3, … bn}
이를 정렬하여 n-tuple 로 나타낸 것을 Ordered basis of V
-> B = (b1, b2, b3,.. bn) 으로 정의
앞의 Coordinates를 보았을 때
Basis Vectors는 일종의 단위이다.
N차원의 Vector space V, V의 Ordered Basis B, $\Phi:R^n \rightarrow V$ 인 Mapping $\Phi$가 있을 때 n차원 실수 공간의 단위 벡터 $(e_1, e_2, \cdot \cdot, e_n)$은 $\Phi$에 의해 $(b_1, b_2, \cdot \cdot, b_n)$로 Mapping 한다.
Transformation Matrix
Vector Space V, W가 있고 그에 대한 Ordered Basis B,C가 각각 있다고 할 때,
$\Phi: V \rightarrow W$인 $\Phi$가 있으면, C로 $\Phi(b_j)$를 다음과 같이 Unique 하게 표현 가능
\(\Phi(b_j) = \alpha_{1j}c_1 + \cdot \cdot + \alpha_{mj}c_{m} = \sum_{i=1}^m \alpha_{ij}c_i\)
이때 모든 j에 대해 $\alpha$를 모으면 $A_{\Phi}(i,j) = \alpha_{ij}$라는 Matrix를 만들 수 있는데 이를 Transformation Matrix라고 부름
Example
Homomorphism한 Vector Space V, W와 그에 대한 Ordered Basis B,C가 각각 있을 때 Linear Mapping $\Phi: V \rightarrow W$에 대해 다음과 같은 식이 성립
\[\Phi(b_1) = c_1 - c_2 + 3c_3 - c_4\] \[\Phi(b_2) = 2c_1 + c_2 + 7c_3 + 2c_4\] \[\Phi(b_3) = 3c_2 + c_3 - 4c_4\]Mapping $\Phi$는 다음과 같은 Matrix로 표현할 수 있음
\[A_{\Phi} = \left [ \alpha_1 , \alpha_2 , \alpha_3 \right ] = \begin{bmatrix} 1 & 2 & 0 \\ -1 & 1 & 3 \\ 3 & 7 & 1 \\ -1 & 2 & 4 \end{bmatrix}\]
Basis Change
기존 $\mathbb{R}^2$ Vector Space의 경우 Basis가 $\begin{bmatrix} 1 \ 0 \end{bmatrix}$ , $\begin{bmatrix} 0 \ 1 \end{bmatrix}$ 인 단위 벡터인데, $\mathbb{R}^2$를 $\begin{bmatrix} 1 \ 1 \end{bmatrix}$ , $\begin{bmatrix} 1 \ -1 \end{bmatrix}$이 basis인 새로운 Vector Space로 Mapping 시킬 경우, $A$ = $\begin{bmatrix} 2 & 1 \ 1 & 2 \end{bmatrix}$이라는 Matrix가 $\tilde{A} = \begin{bmatrix} 3 & 0 \ 0 & 1 \end{bmatrix}$ 라는 좀 더 간단한 대각 행렬로 변한다.
\[\Phi : \mathbb{R}^2 \rightarrow span(\begin{bmatrix} 1 \\ 1 \end{bmatrix},\begin{bmatrix} 1 \\ -1 \end{bmatrix}) 일때,\] \[\Phi(\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}) = \begin{bmatrix} 3 & 0 \\ 0 & 1 \end{bmatrix} = \tilde{A}\]Vector Space V, W와 각각의 Bases B, C와 Linear Mapping $\Phi: V \longrightarrow W$가 있을 때, 다음과 같은 $B$를 $\tilde{B}$로 $C$를 $\tilde{C}$로 Transformation 하는 Matrix를 각각 $S,T$라고 하면 다음 식을 통해서 $\tilde{A_{\Phi}}$를 구할 수 있다.
\[S:B \rightarrow \tilde{B}\] \[T:C \rightarrow \tilde{C}\] \[\tilde{A_{\Phi}} = T^{-1}A_{\Phi}S\]Equivalence : $\tilde{A_{\Phi}} = T^{-1}A_{\Phi}S$인 regular matrix $S \in \mathbb{R}^{nxn}$ 와 $T \in \mathbb{R}^{mxm}$이 존재하면 두 Matrix $A, \tilde{A} \in \mathbb{R}^{mxm}$ 는 서로 Equivalent 하다
Similarity : $\tilde{A} = S^{-1}AS$인 Regular matrix $S \in \mathbb{R}^{nxn}$가 존재하면 두 Matrix $A, \tilde{A} \in \mathbb{R}^{nxn}$는 서로 Similar 하다고 한다
Similar Matrices는 항상 Equivalent 하지만, Equivalent matrices는 항상 Similar 하지는 않다
Example
$\Phi : \mathbb{R}^3 \rightarrow \mathbb{R}^4$ 변환이 있다.
$A_{\Phi} = \begin{bmatrix} 1 & 2 & 0 \ -1 & 1 & 3 \ 3 & 7 & 1 \ -1 & 2 & 4 \end{bmatrix}$ 일때,
표준 bases는
$B = (\begin{bmatrix} 1 \ 0 \ 0 \end{bmatrix},\begin{bmatrix} 0 \ 1 \ 0 \end{bmatrix}, \begin{bmatrix} 0 \ 0 \ 1 \end{bmatrix} ), C = (\begin{bmatrix} 1 \ 0 \ 0 \ 0 \end{bmatrix}, \begin{bmatrix} 0 \ 1 \ 0 \ 0 \end{bmatrix}, \begin{bmatrix} 0 \ 0 \ 1 \ 0 \end{bmatrix}, \begin{bmatrix} 0 \ 0 \ 0 \ 1 \end{bmatrix})$이다.
$\tilde{B} = (\begin{bmatrix} 1 \ 1 \ 0 \end{bmatrix},\begin{bmatrix} 0 \ 1 \ 1 \end{bmatrix}, \begin{bmatrix} 1 \ 0 \ 1 \end{bmatrix} ), \tilde{C} = (\begin{bmatrix} 1 \ 1 \ 0 \ 0 \end{bmatrix}, \begin{bmatrix} 1 \ 0 \ 1 \ 0 \end{bmatrix}, \begin{bmatrix} 0 \ 1 \ 1 \ 0 \end{bmatrix}, \begin{bmatrix} 1 \ 0 \ 0 \ 1 \end{bmatrix})$이다.
-> B, C를 각각 $\tilde{B}$와 $\tilde{C}$로 Transformation 해주는 다음과 같은 Matrix S, T를 구함
$S = \begin{bmatrix} 1 & 0 & 1 \ 1 & 1 & 0 \ 0 & 1 & 1 \end{bmatrix}$
$T = \begin{bmatrix} 1 & 1 & 0 & 1 \ 1 & 0 & 1 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{bmatrix}$
그 후 다음과 같이 $\tilde{A_{\Phi}} = T^{-1}A_{\Phi}S$ 공식을 활용하여 $\tilde{A_{\Phi}}$를 구할 수 있음
\[\tilde{A_{\Phi}} = T^{-1}A_{\Phi}S = \frac{1}{2} \begin{bmatrix} 1 & 1 & -1 & -1 \\ 1 & -1 & 1 & -1 \\ -1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 2 \end{bmatrix} \begin{bmatrix} 3 & 2 & 1 \\ 0 & 4 & 2 \\ 10 & 8 & 4 \\ 1 & 6 & 3 \end{bmatrix}\] \[= \begin{bmatrix} -4 & -4 & -2 \\ 6 & 0 & 0 \\ 4 & 8 & 4 \\ 1 & 6 & 3 \end{bmatrix}\]Image and Kernel
이미지와 커널(Image and Kernel)은 벡터 부분공간에서 중요한 특성이다.
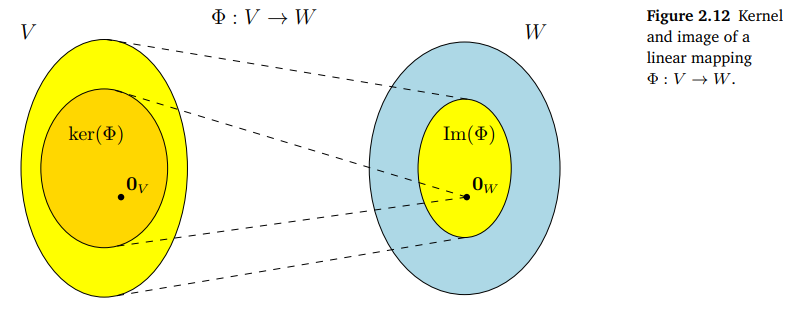
- 이미지(Image)는 vector space V의 어떤 벡터든 vector space W에서 mapping 될 수 있는 W내의 벡터들의 set을 의미한다.\
- 커널(Kernel)은 vector space V의 subset 중에서 vector space W의 null space로 mapping되는 벡터들을 의미한다.
이미지와 커널은 다음과 같은 특성을 가진다.
- 항상 \(\Phi\left(0_{V}\right)=0_{W}\) 이다.
- \({Im}(\Phi)\)는 W의 subspace이고, \({ker}(\Phi)\)는 V의 subspace이다.
- 오직 \(\operatorname{ker}(\Phi)=\{\mathbf{0}\}\)인 경우에만 injective function이다.
영공간과 열공간(Null Space and Column Space)
- $\boldsymbol{A} \in \mathbb{R}^{m \times n}$이고 linear mapping이 \(\Phi: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}, \boldsymbol{x} \mapsto \boldsymbol{A} \boldsymbol{x}\)와 같을 때, A의 Column Space는 결국 Image의 공간과 일치한다.
- \(\operatorname{rk}(\boldsymbol{A})=\operatorname{dim}(\operatorname{Im}(\Phi))\)이다.
- \({ker}(\Phi)\)는 \(A x=0\)의 general solution이다.
Rank-nullity theorem
\[\operatorname{dim}(\operatorname{ker}(\Phi))+\operatorname{dim}(\operatorname{Im}(\Phi))=\operatorname{dim}(V)\]- \(\operatorname{dim}(\operatorname{Im}(\Phi))<\operatorname{dim}(V)\)이면 \(\operatorname{dim}(\operatorname{ker}(\Phi)) \geqslant 1\)
- \(\operatorname{dim}(\operatorname{Im}(\Phi))=\operatorname{dim}(V)\)이면, 다음과 같은 세가지 성격을 가진다.
- \(\Phi\)는 injective, surjective, bijective
'선형대수' 카테고리의 다른 글
-
선형 사상이 주는 대표적인 효과는 기초적인 도형의 변환(회전, 확대, 축소, 대칭)이며, 비선형 사상은 공간이 투영(projective)되거나 불균등 확대(Non uniform scaling) 등 일반적으로 모양이 보존되지 않는다. ↩