선형대수
Introduction : Linear Algebra
선형대수
선형대수(Linear Algebra)는 벡터와 벡터공간, 벡터를 다루는 방법들을 연구하는 대수학의 한 분야이다.
여러 머신 러닝 알고리즘들, 특히 딥러닝 알고리즘들을 이해하고 사용하려면 선형대수를 잘 알아야할 필요가 있다.
선형대수에 본격적으로 들어가기에 앞서, 가장 필수적인 개념인 벡터에 대해 먼저 소개를 하려고 한다.
보통 학교에서 배우고, 우리가 일반적으로 알고있는 벡터는 기하 벡터(geometric vector)라고 불리우며, 다음과 같이 표현한다.
\[\vec {x}, \vec {y}\]이 책에서 다루는 벡터는 보다 일반적인 관점에서의 벡터를 의미하는데, 다음과 같이 굵은 글자를 사용하여 표현한다.
\[\boldsymbol {x}, \boldsymbol {y}\]일반적인 관점이 무슨말이냐 하면, 벡터를 정의할 때 서로 더하거나 실수를 곱하여 같은 타입의 벡터가 만들어지면 모두 벡터라고 간주한다.
다음과 같은 예시들을 보고 같이 이해해보도록 하자.
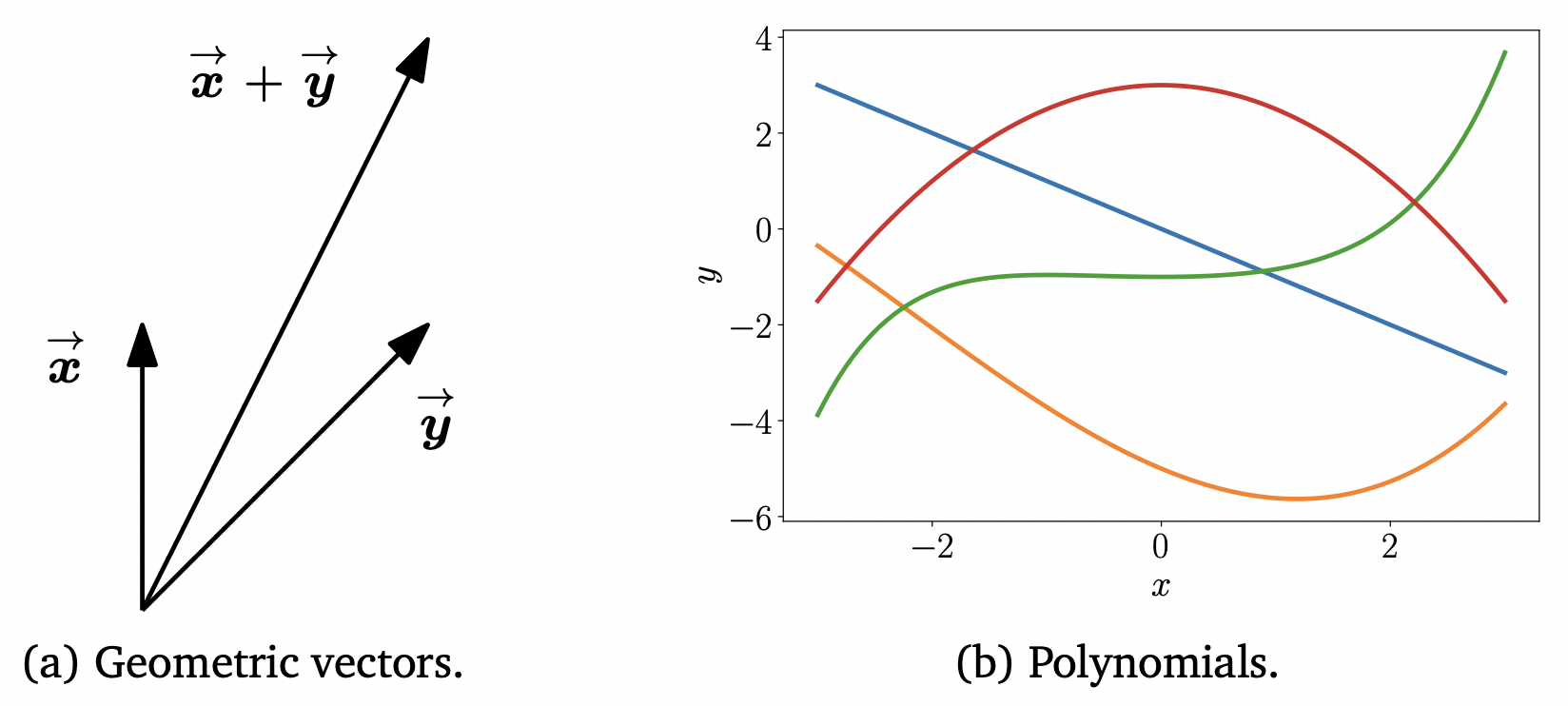
그림1 (a) 기하학적 벡터(Geometric vectors) (b) 다항식(Polynomials)
-
기하학적 벡터(Geometric vector) : 그림1 (a) 을 보면 꽤 익숙한 모양의 벡터를 볼 수 있다. 우리가 일반적으로 알고 있는 벡터인 기하학적 벡터로, 두 벡터끼리 더하거나 스칼라값을 곱해도 또 다른 벡터가 되므로 벡터로 정의된다.
-
다항식(Polynomials) : 그림1 (b) 의 다항식도 벡터이다. 두 다항식을 더해 새로운 다항식을 만들 수 있고, 스칼라값을 곱하면 그 역시 다항식이 되기 때문이다. 물론, 기하학적 벡터에 비해 추상적인 개념이지만 일반적인 관점에서의 벡터라고 한다.
-
오디오 신호(Audio signals) : 오디오 신호는 연속적인 숫자로 표현되기 때문에, 오디오 신호끼리 더할 수 있다. 오디오 신호의 합은 새로운 오디오 신호가 되며, 스케일링으로 스칼라값을 곱하면 역시 새로운 오디오 신호를 얻을 수 있다. 그러므로, 오디오 신호도 벡터의 한 종류이다.
-
$\mathbb{R}^n$의 요소들도 일반적인 관점에서의 벡터가 된다. 추상적인 개념이기에 예시와 함께 보자면,
다음과 같이 구성된 \(a = \left[ \begin{matrix} 1 \\ 2 \\ 3 \\ \end{matrix} \right] \in \mathbb{R}^3\) 를 생각해보자.
$ a, b \in \mathbb{R}^n $ 일때, 성분별(component-wise)로 더해준 결과값은 벡터가 된다 : $ a + b = c \in \mathbb{R}^n $
마찬가지로, $ a \in \mathbb{R}^n $ 와 스칼라 값인 $ \lambda \in \mathbb{R} $ 를 곱해주면 $ \lambda a \in \mathbb{R}^n $ 으로 스케일링된 벡터가 된다.
선형대수에서는 이렇게 일반적인 벡터의 개념을 사용하여 대부분의 알고리즘이 $\mathbb{R}^n$ 영역에서 이루어진다.
이 책에서도, $\mathbb{R}^n$ 영역에서의 벡터에 초점을 맞추어서 이야기를 풀어나가고 있다.
벡터의 닫힘성(Closure)
닫혀있다(Closed)는 말은 수학에서 중요한 속성 중 하나이다.
벡터가 닫혀있다는 의미는 벡터 집합을 서로 더하고 스케일링함으로써 얻을 수 있는 벡터 집합을 의미한다.
이렇게 얻어진 집합을 벡터 공간(Vector Space)이라고 하며 2.4에서 자세히 소개하고 있다.
그리고, 이번 장에서 다룰 내용들에 대한 마인드맵은 아래와 같으니 참고해도 좋을 듯 하다.
그림2 Chapter2 선형대수학 마인드맵
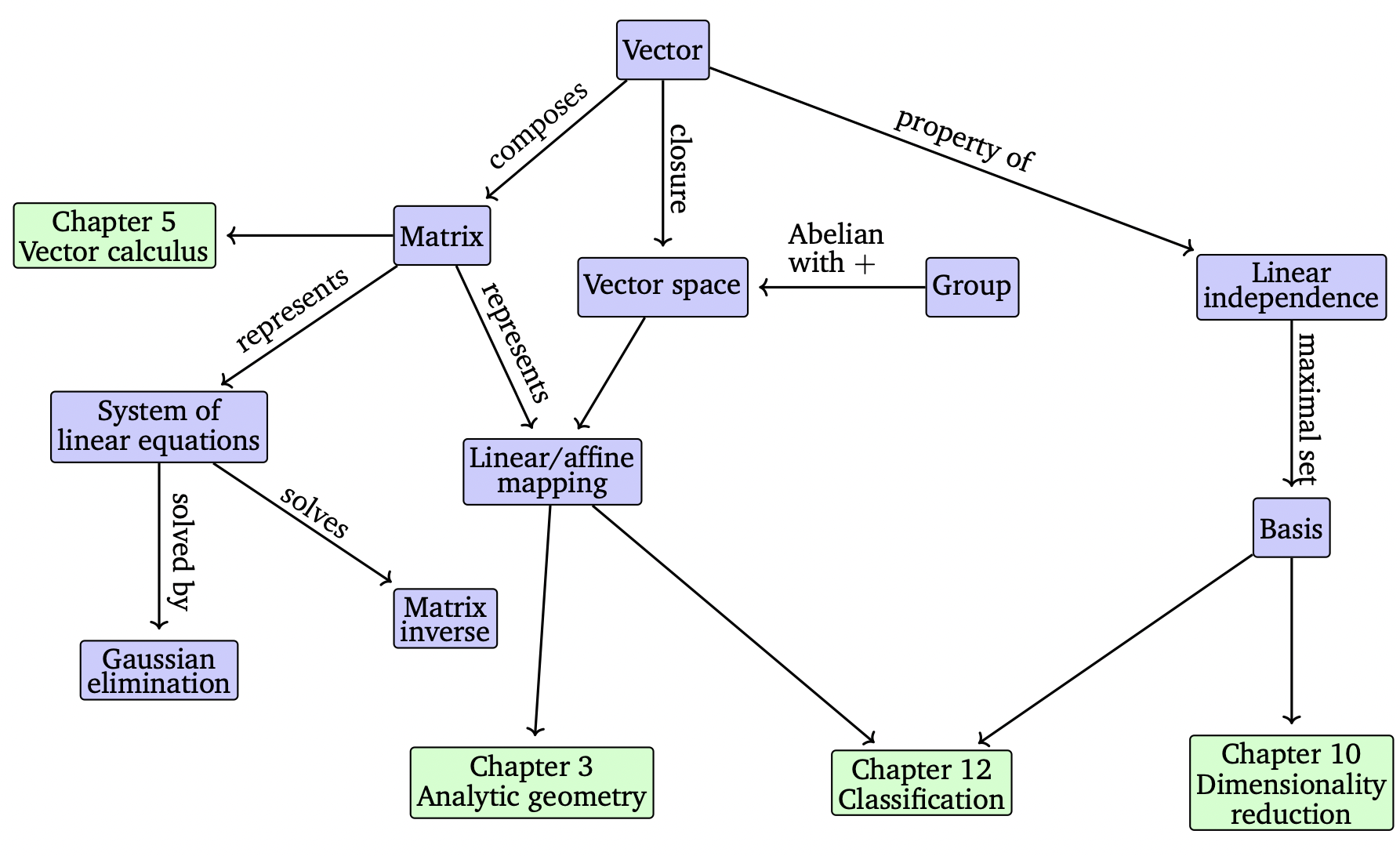
추가적으로, 이 책의 내용 외에도 좋은 컨텐츠들을 소개하면서 마치도록 하겠다.