놈
Chapter 1 : Norm
Edited by / 임수형 (sulogc) 
놈의 정의
일반적으로 벡터의 길이는 시점과 종점사이의 거리로 생각할 수 있다. 벡터의 길이는 수학에서 절대값의 일반화된 형태인 놈으로 정의 할 수 있다.
벡터 공간 V상에서의 놈은 다음을 만족하는 함수로 정의된다.
\[\begin{align} \lVert \cdot \rVert : V \to \mathbb{R} \\ x \mapsto \lVert x \rVert \end{align}\]이는 각각의 벡터 $x$에 대해 길이 $\lVert x \rVert \in \mathbb{R} $을 반환하는 연산으로 이해할 수 있다.
놈의 성질
$\lambda \in \mathbb{R}$ 와 $ x, y \in V$ 에 대해 다음 성질을 가진다.
- 양의 동차성: $ \lVert \lambda x \rVert = \lvert \lambda \rvert \lVert x \rVert$
- 삼각 부등식: $ \lVert x + y \rVert \le \lVert x \rVert + \lVert y \rVert $
- 양의 정부호성: $ \lVert x \rVert \ge 0 $ $ and $ $ \lVert x \rVert = 0 \iff x = 0 $
임의의 상수 곱에 비례하다는 것과, 길이이기 때문에 삼각부등식을 만족하며, 양 정의되어 있다는 것을 확인 할 수 있다. 벡터의 길이를 측정하는 다음 두 가지 놈을 알아보자.
놈의 종류
그림1 Norms
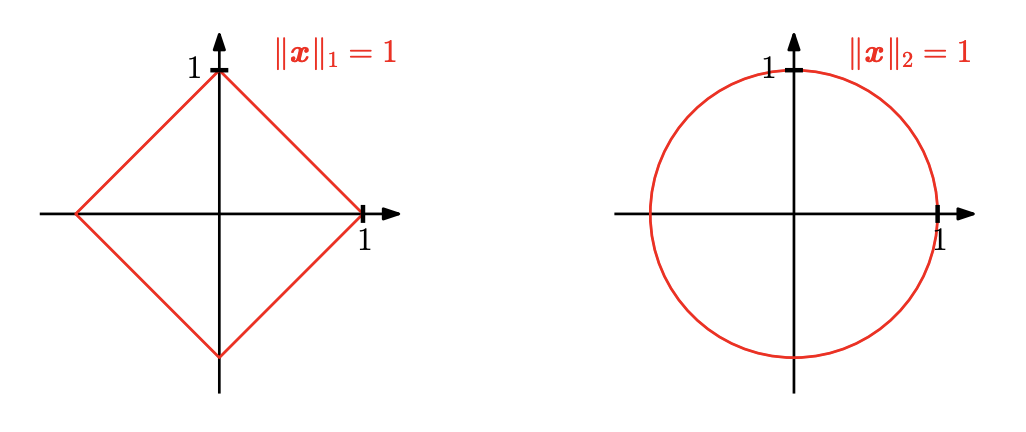
맨해튼 놈 ( $l_1$ norm)
$ \mathbb{R}^n $ 상에서 맨해튼 놈은 다음과 같이 정의된다.
\[\lVert x \rVert _1 = \sum_{i=1}^n \lvert x_i \rvert ,\]여기서 $\lvert \cdot \rvert$ 은 절대값을 연산이다. 그릠 1 에서 보는 것 과 같이 격자 거리임을 알 수 있다.
유클리디안 놈 ( $l_2$ norm)
$ \mathbb{R}^n $ 상에서 유클리디안 놈은 다음과 같이 정의된다.
\[\lVert x \rVert _2 = \sqrt{ \sum_{i=1}^n x_i^2 } = \sqrt{x^T x}\]각 원소를 제곱하여 $ \sqrt{x^T x} $ 를 통해 연산가능 하다. 그림 1 에서 보는 것과 같이 실 거리로 많이 측정되는 유클리드 거리임을 알 수 있다.