문제 정의
Chapter 1 : Problem Setting
Edited by / 박상은 (CheezEun) 
장성준 (junnei) 
문제 정의(Problem Setting)
우리의 목표는 PCA를 이용하여 $D$ 차원의 데이터 $x_n$ 을 정보 손실을 최소화하면서 축소하여 $M$차원의 저차원 데이터 $z_n$ ($M < D)$로 만드는 것이다. 이 때, $z_n$을 통해 다시 복원한 데이터 $\tilde{x}_n$ 는 $x_n$ 과 유사한 $D$ 차원의 데이터여야 하며, 이는 $M$차원의 subspace $U \subseteq \mathbb{R}^D$에 속하는 데이터이다.
이전 페이지의 (10.3), (10.5), (10.6) 와 아래의 예시를 통해 PCA에 대해 설명하자면 다음과 같다.
[그림 3] Schematic and example of PCA
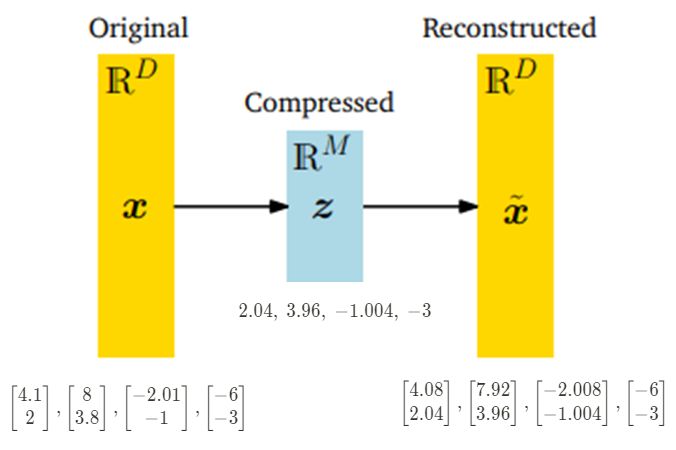
위의 예제에서, 차원축소를 위한 $M$개의 Orthonormal basis (ONB) $(b_1 , b_2, \cdots, b_M)$ 에 대해
basis $B := [b_1 , b_2, \cdots, b_M]$$\in \mathbb{R}^{D \times M}$ 라고 하면 다음과 같은 식이 성립한다.
\[z_n = B^\textsf{T} x_n \in \mathbb{R}^M \tag{10.7}\] \[\tilde{x}_n = Bz_n = BB^\textsf{T} x_n \in \mathbb{R}^D \tag{10.8}\]이 때의 encoder ($x_n \rightarrow z_n)$ 및 decoder ($z_n \rightarrow \tilde{x}_n$) 역할을 수행하는 basis $B$ 를 구하는 것.
이것이 바로 PCA의 최종 목표라고도 할 수 있다.
아래에 이어지는 [10.2]와 [10.3]에서는 서로 다른 과정을 통해 basis $B$를 구할 것이다.
[10.2] 에서는 보존되는 정보(=분산)를 최대화시키는 과정을 통해서,
[10.3] 에서는 손실(=projection loss)을 최소화시키는 과정을 통해서 접근한다는 점이 특징적인 차이점인데,
두 가지 접근법을 통해 결론적으로 밝히고자 하는 바는
$X$에 대한 covariance $S$의 eigenvector 방향으로 orthogonal projection하는 것이
정보의 손실을 최소화시키면서 차원을 축소시키는 것이라는 내용이다.