이산 확률과 연속 확률

Chapter 2 : Discrete and Continuous Probabilities

Edited by / 김주원 (Kim-Ju-won)

확률 함수

이번 섹션에서는 섹션6.1에서 소개된 바와 같이 사건의 확률 표현 방법에 대해서 설명한다. Target Space가 이산형(Discrete)인지 혹은 연속형(Continous)인지에 따라 확률분포를 접근하는 방법이 달라진다.

확률질량함수(probability mass function)

Target Space $T$가 이산형(Descrete)할 때 확률 $x \in T$f로 특정할 수 있고 확률 변수 $X$가 $P(X = x)$로 나타낼 수 있다. 이 때 이산형 확률 변수(Descrete Random Variable) X에 대한 함수 $P(X = x)$는 확률 질량 함수(probability mass function)라고 한다.

누적분포함수(cumulative distribution function)

Target Space $T$가 연속형(Continous), 일차원 함수 처럼 확률 변수 $X$를 특정 범위내의 확률로 정의하는게 자연스럽다. 따라서, 일반적으로 확률 변수 X를 $P(a \leq X \leq b)$ (단,$a<b$)로 나타낸다. 또는 확률 변수 $X$는 $P( X \leq x)$로 표기하며 $x$ 보다 작을 확률을 의미한다. 연속 확률 변수 $X$에 대한 $P( X \leq x)$를 누적분포함수(cumulative distribution function)라고 한다.

참고1. 단일변수(Univarate), 다변수(multivarate) 분폰

univariate distribution를 하나의 확률변수에 대한 분포로 사용할 것이다(state는 non-bold x로 나타낸다). 두개 이상의 확률변수에 대한 분포는 multivariate 분포로 사용할 것이며, 확률변수를 벡터를 이용한다(state는 bold x로 나타낸다)

이산 확률(Discrete Probabilities)

Target space가 이산형(Discrete)일 때 아래 그림과 같이 확률 분포를 다차원 배열을 여러개의 확률변수로 채우는 것으로 생각해볼 수 있다.

그림1 CHAPTER 6 확률밀도함수 다차원배열 시각화

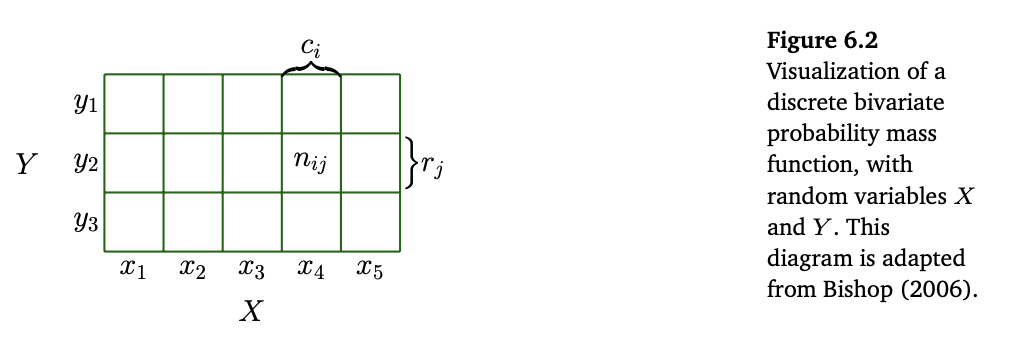Target space의 joint probability(결합확률)는 각 확률변수의 target space에 대한 데카르트 곱(Cartesian Product)로 볼 수 있다. 이는 다음식과 같이 정의 된다.

\[P(X=x_i,Y =y_j)= \frac {n_{ij}} N\]

$n_{ij}$는 $x_i$와 $y_j$ 사건이 동시에 일어나는 경우의 수이며, $N$은 모든 경우의 수를 말한다. 따라서 결합확률은 다음과 같이 표기할 수도 있다.

\[P(X =x_i,Y =y_j)=P(X =x_i ∩Y =y_j)\]

앞서 본 그림1은 확률 밀도함수(pmf)를 시각화 한것으로, 확률변수 $X,Y$에 대해 $X=x_i, Y =y_j$에 대한 확률 값으로 $p(x,y)$로 표기 할 수 있다. 또한

주변확률 분포(marginal distribution) : 확률변수 $X,Y$에 대해 서로에 무관한 값을 취하여 나타내는 확률분포를 $p(x)$라고 쓴다. $X ∼ p(x)$ 는 확률 변수 $X$가 $p(x)$에 의해 분포될 때 사용한다.
조건부 확률(conditional distribution) : 한 확률 변수를 고정하고 다른 확률변수에 대한 확률을 구하는 것을 조건부 확률이라고 하며 $p(x|y)$로 표기한다.

예시1) 그림 1과 같이 두개의 확률변수 $X,Y$에 대해서 $X$는 5가지 가능한 상태가 있고, $Y$는 3가지 가능한 상태가 있다고 가정하자. $n_{ij}$는 $X =x_i$,$Y =y_j$인 경우라 하고, $N$을 모든 경우에 대한 확률 변수라고 가정하자. 이 때 $c_i$를 $i$번째 행의 합 $c_i=\sum_{j=1}^3 n_{ij}$라고 하고, 이 때 $r_i$를 $i$번째 행의 합 $r_i=\sum_{i=1}^5 n_{ij}$라고 하면 확률 변수 $X,Y$에 대한 주변확률분포(marginal distribution)과 조건부 확률(Conditional Probability)를 명확하게 구할 수 있다.

주변확률분포(marginal distribution)
$P(X=x_i)= \frac {c_i} {n_{ij}} = \frac {\sum_{j=1}^3 n_{ij}} N$
$P(X=x_i)= \frac {r_j} {n_{ij}} = \frac {\sum_{i=1}^5 n_{ij}} N$

조건부 확률(Conditional Probability) : 각 행, 열을 하나의 셀(cell)로 취급하면 다음과 같이 구해줄 수 있다.

$X$가 주어졌을 때 조건부 확률 $P(X =y_j | Y =x_i) = \frac {n_{ij}} {c_i}$
$Y$가 주어졌을 때 조건부 확률 $P(X =x_i | Y =y_j) = \frac {n_{ij}} {r_j}$

참고2. 머신러닝과 이산확률

머신러닝에서 이산확률은 범주형 변수(categorical values)를 다룰 때 사용한다. 예를 들어 범주적 특징을 가진 대학의 학위를 이용해서 연봉을 예측 한다던지, 필기 인식을 위한 알파벳의 범주적 라벨링 같은 것들을 이용한다. 또한 이산형 변수는 유한한 연속확률분포를 결합한 모델링에도 자주 사용된다.(Section 11)

연속 확률(Continuous Probabilities)

정의 및 유의사항

이 섹션에서 확률변수는 실제 값(real-valued)을 고려한다. 따라서 Target Space는 실수 ${R}$에 안에 있는 선형구간에서 고려한다. 연속 확률 변수를 유한한 크기의 이산 확률 공간을 가진 것처럼 연산을 할 수 있다고 가정한다. 그러나 이러한 가정은 다음 두 가지 상황에서는 정확하지 않는다.

어떤 실험을 무한히 자주 반복하고 싶은 경우
- 기계 학습에서 일반화 오류를 논의할 때 발생한다(Section 8)
$R$의 구간내에서 점을 점으로 표현하고 싶은 경우
- 두번째 상황은 가우스와 같은 연속 확률분포에 대해 논의할 때 발생.(Section 6.5)

직관적인 이해을 돕기 위해, 정확성이 부족하더라도 해당 개념에 대해 간단한 소개를 진행하였다. 따라서 유의하여 읽어주길 바란다.

참고3. 연속확률과 비선형적인 기술

연속확률 공간에서필요한 두가지 비선형적인 기술이 있다.

1.사건 공간을 정의하는데 사용되었던 모든 부분 집합은 잘 작동하지 않는다.사건 공간은 여집합, 교집합, 합집합에 대해 잘 동작하도록 제한될 필요가 있다

2.이산확률의 원소들을 세는 작업으로 만들었던 연속확률 공간의 확률을 다루기 어렵다는 사실이다.해당 공간(집합)의 크기를 측정값(measure)이라고 부른다. 예를 들어 이산집합의 구간, 부피 모두 측정값(measures)으로 부른다. 집합 연산이 잘 작동하며 체계성을 갖춘 집합을 Borel σ-algebra라고 부른다.

Betancourt는 기술적 문제에 얽매이지 않고 집합론으로 확률 공간의 구성을 자세히 설명한다.(https://tinyurl.com/yb3t6mfd). 정확한 확률공간의 정의는 Billingsley (1995) and Jacod and Protter (2004)을 참고하면 된다

이 확률 공간에서 실제 값(real-valued)를 가진 확률변수들은 Borel σ-algebra를 따른다. 또한 $R^D$의 확률 변수들은 확률 변수 벡터로 간주한다.

정의 1 : 확률밀도함수(Probability Density Function)

함수 $f : \mathbb{R}^D \rightarrow \mathbb{R}$는 확률밀도함수(Probability Density Function)라고 부르며, $pdf$라고 부른다. 그리고 다음을 만족한다.

$\forall x\in \mathbb{R}^D$
적분을 가능해야하며 $\int_{\mathbb{R}^D} f(x)dx=1$ 을 만족해야한다.

참고4. 이산확률 변수와 확률 질량함수

이산확률 변수의 확률 질량 함수(pmf)인 경우 적분(intergra)이 합(summation)으로 대체 된다.

모든 확률 밀도 함수의 적분 값은 음의 값을 가질 수 없으며 1이다. 아래의 식 $a,b \in \mathbb{R}$이고 $x \in \mathbb{R}$이고 연속 확률 변수의 결과값은 다음과 같은 식으로 표현한다.

\[P(a \leq X \leq b) = \int_a^b f(x)dx=1\]

States $x \in \mathbb{R}^D$도 $x \in \mathbb{R}$도 유사하게 정의된다. 그리고 이러한 관계를 law 또는 분산(distribution)이라고 부른다.

참고5. 연속 확률 변수와 확률 질량 함수

이산 확률 변수와 다르게 연속 확률 변수 X가 특정 값 x에서의 확률P(X = x)는 0이다. 이는 해당 적분 구간의 범위를 a = b와 같게 하기 때문이다.

누적 분포 함수(Cumulative Distribution Function)

정의 1 : 누적 분포 함수(Cumulative Distribution Function) $x \in \mathbb{R}^D$를 만족하는 multi-variate 확률 변수 $X$의 누적 분포 함수(cdf)는 다음과 같다.
$F_X(x) = P(X_1 \leq x_1,...,X_D \leq x_D)$
위 식은 $X = [X_1,…,X_D]^⊤, x = [x_1,…,x_D]^⊤$를 만족하며, 우변은 확률 변수 $X_i$가 $x_i$보다 작거나 같은 경우의 확률을 의미한다.

누적분포 함수(cdf)는 다음과 같은 확률 밀도 함수(the probability density function)의 적분으로도 표현할 수 있다.

\[F_X(x) =\int_{-\infty}^{x_i} ...\int_{-\infty}^{x_D} f(z_1, ..., z_d)dz_1...dz_d\]

참고6. 유의사항

1.우리는 두가지 구별된 다른 확률분포를 공부하고 있다는 걸 명심해야한다. 첫 번째로 확인한 건 f(x)로 명시된 pdf는 양의 함수이고, 적분하면 1이되야 된다는 것이다. 두번째는 확률 변수 X와 pdf f(x)의 관계이며, 확률 변수 X에 대한 law라는 것이다.

2.pdf가 없는 cdf가 있다는 사실도 유의해야 한다.

이 책에서는 $f(x)$와 $F_X(x)$를 구분해서 사용하지 않는다. 그 이유는 pdf와 cdf를 대개의 경우 구분하지 않기 때문이다 .하지만 Section 6.7에서는 해당 개념에 대해서 구분해서 생각해야 할 것이다.

이산 확률 분포와 연속 확률 분포의 구분(Contrasting Discrete and Continous Distributions)

앞에서 언급하였듯이 확률은 양수이며 모든 가능한 확률의 합은 1이다.(Section 6.1.2). 이산 확률 변수에서 확률은 구간 [0,1]사이에 있어야 한다. 연속 확률 변수에서 확률 변수의 값은 1보다 클수도 있다. 해당 내용을 이산 균등 분포, 연속 균등 분포 그림에서 확인할 수 있다.

그림2 CHAPTER 6 이산균등분포와 연속균등분포

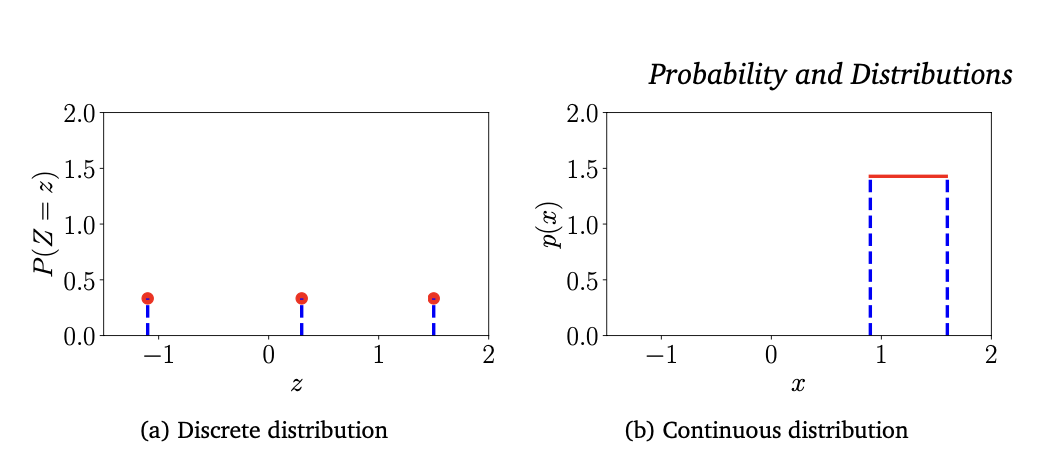
예시 1 이 예시에서는 모든 확률이 동일하게 일어나는 균등분포를 가정한다. 그리고 이 균등분포에서 이산/연속 확률 변수의 차이점을 살펴보자 $Z$를 이산 균등 분포의 확률변수라고 가정하자. 해당 값은 아래와 같이 ${z = −1.1, z = 0.3, z = 1.5}$를 가진다. 그렇다면 이 확률변수의 확률 질량 함수는 아래와 같다.

또는 이 함수를 그림2에서의 확률 변수를 $x$축으로 하고 확률을 $y$축으로 하는 (a)그래프라고 생각해줄 수 있다. 이처럼 연속 확률 변수에 대한 그래프는 확률 변수를 $x$축으로 하고 확률을 $y$축으로 하는 (b)그래프라고 생각해줄 수 있다. 그래프를 통해 $0.9\leq X \leq 1.6$ 구간의 확률 값은 1보다 클 수 있음을 알 수 있지만, 적분 값은 최대 1이 넘지 않는다.

\[\int_{0.9}^{1.6} f(x)dx=1\]

참고7. 유의사항

1.이산 확률 분포에 유의점이 있다. Z의 값들은 어떤 구조도 갖지 않는다. 구분지어줄 수 없다는 것인데, 머신러닝에서는 예시와 같이 값이 부여되어 대소가 생겨 비교할 수 있게 된다. 그리고 이러한 숫자 값을 지정하게 되면, 이산변수의 값은 확률의 기댓값을 고려할 수 있게 되어 유리한 측면디 있다.

2.부정확하더라도 '확률분포'(descrete distribution)이라는 표현을 이산 확률 변수의 pmf뿐만이 아니라 연속확률 변수의 pdf를 나타내는데도 책에서는 활용된다. 따라서 맥락을 통해 해당 개념을 확인해야한다.

머신러닝에서 표본공간 $\Omega$, 사건 공간 $T$, 확률 변수를 구분해서 표기하지 않는다. 확률 변수 $X$가 가능한 모든 결과 값은 $x \in T , p(x)$로 임의의 확률 변수 $X$가 가질 변수를 의미합니다. 이산 확률 변수의 경우 이를 확률 질량 함수라고 하는 $P(X = x)$로 쓴다. 이산확률 변수의 확률 질량 함수(pmf)와 연속 확률 변수의 확률 밀도 함수(pdf)는, 또한 더 나아가 누적 분포 함수(cdf)도 확률(distribution)라고 대신 쓸 것이다.

또한 $X$를 단일/다변수 확률 변수를 표기할 것이며, 해당 부분에 대해서 정리한 것은 아래의 표와 같다.

타입(Type)	점 확률(point probability)	구간 확률(Interval Probability)
이산(Discrete)	$P(X=x)$ 확률질량함수(pmf)	해당 사항 없음
연속(Continuous)	$p(x)$확률밀도함수(pdf)	$P(X \leq x)$ 누적분포함수(cdf)

'확률 분포' 카테고리의 다른 글